Следует отметить, что первое
включениегораздо![]() продолжительнее остальных импульсов
продолжительнее остальных импульсов ![]() , таккак в момент начала первого включения сигнал обратной связи начинает,
возрастать с нуля, что требует
большего времени для достижения порога отключения релейного элемента.
, таккак в момент начала первого включения сигнал обратной связи начинает,
возрастать с нуля, что требует
большего времени для достижения порога отключения релейного элемента.
Под действием управляющих импульсов ![]() ,
формируемых регулирующим блоком,
исполнительный механизм постоянной скорости будет пере-
,
формируемых регулирующим блоком,
исполнительный механизм постоянной скорости будет пере-
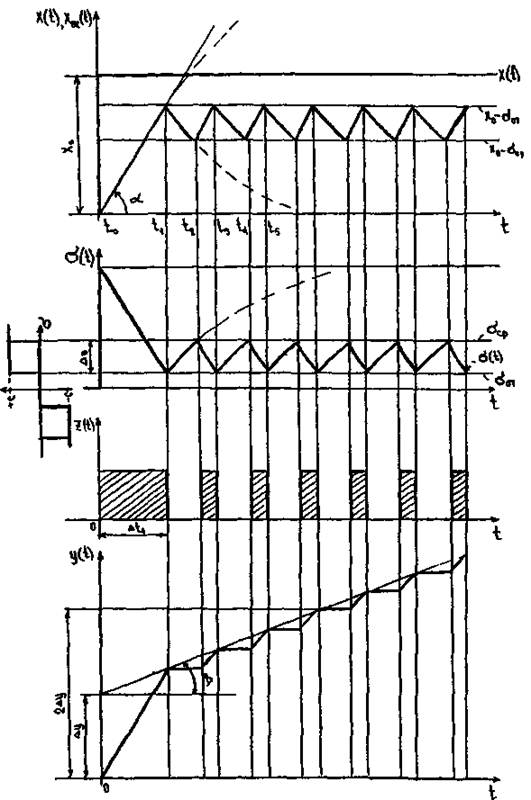
Рис.6
где 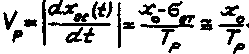 -скорость
разряда цепи обратной связи
-скорость
разряда цепи обратной связи
при отключении РЭ.
Допуская ![]() f которое обычно
выполняется, получаем:
f которое обычно
выполняется, получаем:
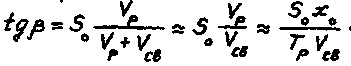 (14)
(14)
Подстановка (II) и (14) в (9) и (10) дает
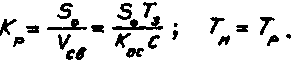 (15)
(15)
Как видно, ![]() зависит от скорости
исполнительного механизма
зависит от скорости
исполнительного механизма ![]() и скорости связи
и скорости связи ![]() (начальной скорости заряда в цепи
ЮС), а
(начальной скорости заряда в цепи
ЮС), а ![]() численно разно постоянней времени
разряда цепи ОС
численно разно постоянней времени
разряда цепи ОС![]()
Очевидно, что разделение цепей
заряда и разрядка формирующей обратной
связи приводит к независимости органов настройки параметров регулятора ![]() и
и ![]() .
При
.
При ![]() и
и ![]() однозначно
взаимосвязаны, т.е. определяются одним
однозначно
взаимосвязаны, т.е. определяются одним![]() органом настройки.
органом настройки.
Выражения (13) показывают, что длительность импульса ![]() практически не зависит от значения
входного сигнала
практически не зависит от значения
входного сигнала ![]() , тогда как длительность
, тогда как длительность ![]() обратно пропорциональна
обратно пропорциональна ![]() . При этом скважность
. При этом скважность
![]() управляющих импульсов
управляющих импульсов ![]() зависит от
зависит от ![]() практически линейно. Следовательно,
регулирующий блок вместе с исполнительным механизмом постоянной скорости реализует закон
регулирования, близкий к линейному ПИ-закону.
практически линейно. Следовательно,
регулирующий блок вместе с исполнительным механизмом постоянной скорости реализует закон
регулирования, близкий к линейному ПИ-закону.
1.6. Структурнея схема замкнутей АСР
Замкнутая одноконтурная АСР может быть условно разделена на регулируемую и регулирующую части. К регулируемой части относится объект регулирования, в соства которого при расчетах и экспериментах включаются кроме технологического объекта регулирующий орган и датчик, измеряющий значение регулируемой величины. К регулирующей части относится регулирующий прибор с исполнительным механизмом.
Структурная схема одноконтурной АСР
при таком делении имеет вид, показанный на рис. 7. Динамические свойства
отдельных элементов системы, знание которых необходимо для настройки
регулятора, могут быть выражены в виде двух передаточных функций ![]() и
и![]()
Дифференциальное уравнение и передаточнзя функцияидеального ПИ-регулятора известны и могут быть использованы для расчетов, а динамические свойства объекта регулирования неизвестны, но их можно определить экспериментально.
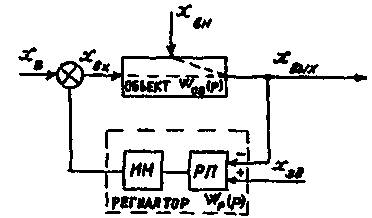
Рис.7
1.7. Экспериментальное определение динамических характеристик объекта
Простейший способ выражения
динамических свойств объекта регулирования - переходная характеристика,
представленная графиком изменения во
времени выходной регулируемой величины вызванного ступенчатым изменением
входной величины![]() (см. рис. 3). Величины и
(см. рис. 3). Величины и![]() отсчитываются от значений,
установившихся до нанесения
отсчитываются от значений,
установившихся до нанесения![]() возмущения.
возмущения.
Часто используют переходную характеристику![]() ,
приведенную к единичному ступенчатому
возмущению. В линейной системе
,
приведенную к единичному ступенчатому
возмущению. В линейной системе

не зависит от исходного значения![]() ,
величины и направления возмущения на входе
,
величины и направления возмущения на входе![]()
Для объекта с самовыравниванием,
переходная характеристика которого
показана на рис. 8, ![]() (коэффициент передачи объекта). При
экспериментальном определении переходных характеристик необходимо выполнить
следующие условия:
(коэффициент передачи объекта). При
экспериментальном определении переходных характеристик необходимо выполнить
следующие условия:
1) перед нанесением возмущения добиваются установившегося (невозмущенного) состояния объекта, что особенно важно при малом числе экспериментов. Это достигают стабилизацией входной величины, нагрузки и других величин, влияющих на измеряемую входную величину. Желательно, чтобы перед опытом такая входная величина, как температура поддерживалась постоянной в течение I...2 мин;
при исследовании динамических
свойств объекта, с целью настройки
регулятора, возмущение может наноситься со стороны регулирующего органа![]() или изменением задания регулятору
или изменением задания регулятору![]()
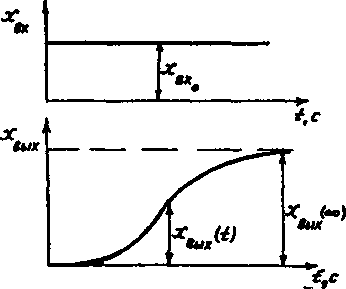
Рис.8
3) возмущение должно наноситься мгновенно. Если мгновенное нанесение возмущения невозможно, необходимо учитывать длительность егс нанесения и за начале отсчета времени изменения выходной величины принимать 1/2 времени нанесения возмущения;
4) опыт заканчивают при достижении нового установившегося значения выходной регулируемой величины.
Результаты каждого вксперимента
содержат элементы случайности из-за помех, которые всегда имеются в реальном
объекте. Для исключения влияния
случайных факторов на экспериментальные характеристики производят
статистическую обработку полученных результатов усреднением большого количества результатов при одинаковой входной
ситуации. Для этого полученные экспериментальные данные совмещают, на
одном графике (рис. 9) и строят усредненную кривую![]() ;
;
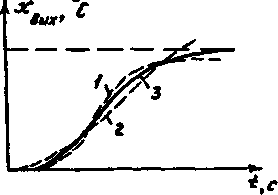
![]()
где ![]() - число опытов;
- число опытов; ![]() - номер опыта.
- номер опыта.
Полученную кривую можно преобразовать
в переходную характеристику ![]() , приведенную к единичному
возмущению (16). По экспериментальной
переходной характеристике можно
определить передаточную функцию объекта.
, приведенную к единичному
возмущению (16). По экспериментальной
переходной характеристике можно
определить передаточную функцию объекта.
В первом приближении объект с самовыравниванием может быть аппроксимирован двумя элементарными звеньями - апериодическим звеном и звеном запээдывания, включенными последовательно. При такой упрощенной замене дифференциальное уравнение объекта:
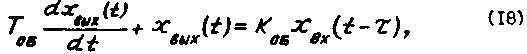
Передаточная функция
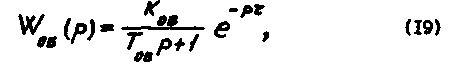
коэффициент передачи объекта![]() ;
;
 (20)
(20)
![]() - постоянная
времени объекта, с;
- постоянная
времени объекта, с; ![]() - запаздывание, с. Значение коэффициентов
- запаздывание, с. Значение коэффициентов ![]() дифференциального
уравнения объекта могут быть определены по графику переходной характеристики.
Проще всего, хотя и с малой точностью
дифференциального
уравнения объекта могут быть определены по графику переходной характеристики.
Проще всего, хотя и с малой точностью ![]() и
и
![]() можно определить графически, как показано на рис. 10. Касательная к кривой
приведена в точке ее перегиба.
можно определить графически, как показано на рис. 10. Касательная к кривой
приведена в точке ее перегиба.
Здесь![]() - значение подкасательной;
- значение подкасательной;
![]() -
это статическая характеристика
объекта регулирования.
-
это статическая характеристика
объекта регулирования.
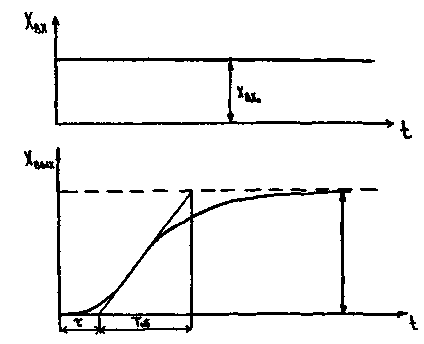
Рис. 10
1.8. Расчет параметров динамической настройки регулятора на заданный переходный процесс в АСР
Зная динамические свойства объекта и
ПИ-регулятора, можно определить настройки регулятора и ![]() на желаемый вид переходного процесса в АСР после возмущения.
на желаемый вид переходного процесса в АСР после возмущения.![]() Расчет этих параметров - сложная
задача, но для простейших объектов, динамические свойства которых
Расчет этих параметров - сложная
задача, но для простейших объектов, динамические свойства которых
выражены двумя элементарными
звеньями (1.9), можно воспользоваться готовыми расчетами, результаты которых
сведены в табл. I, составленную для трех типовых переходных процессов в замкнутой АСР (рис. II) -граничного апериодического
процесса I с минимальным временем регулирования; процесса 2 с 20SS-M перерегулированием(![]() )
)
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.