Номинальные технические данные электродвигателя. Функциональная схема якорного канала двухзонной системы автоматического управления с подчиненными контурами регулирования токов якоря и возбуждения двигателя постоянного тока независимого возбуждения, страница 7

                                                                     ^W_рт.   (3.5) р

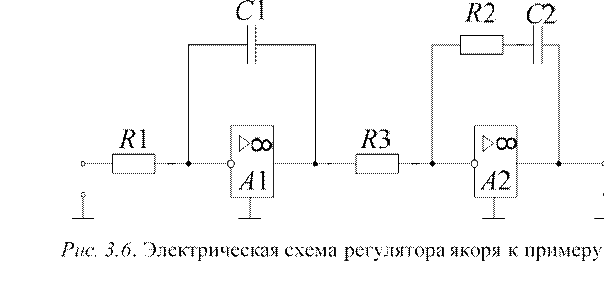
В Приложении 3 представлены типовые регуляторы линейных САУ электроприводов. Из него можно найти, что синтезированный регулятор тока якоря представляет собой последовательное соединение И-регулятора и ПИ-регулятора, схема которого изображена на рис. 3.6. Передаточная функция этой схемы:

⎛ 1 ⎞ ⎛ R²C² p +1⎞⎟⎟. (3.6)  W_сх(р) = ⎜⎜⎝ R₁C₁p ⎟⎠⎟ ⎜⎜⎝ R₃C₃ p ⎠

Сопоставляя (3.5) и (3.6), получим уравнения определения параметров регулятора:

1

                                            K_рт = = 526;

R1C1R3C3

                                          Т_рт = R₂C₂ = 44,3⋅10⁻³ c.

Система уравнений недостаточна, поэтому зададим ряд резисторов и конденсаторов с наиболее часто употребляемыми величинами сопротивлений и емкостей: 

                         R₁ = 100 кОм;   R₃ = 1 Мом;   С₂ = 0,1 мкФ.

Тогда R₂ = Т_рт/С₂ = 44,3· 10^–3 / 0,1 · 10^–6 = 44,3 · 10⁴ Ом = 443 кОм,

CмкФ.

             R₁R₃C₂К_рт           100⋅10 ⋅1⋅10 ⋅0,1⋅10       ⋅526

По шкалам резисторов и конденсаторов (Приложение 4) выберем ближайшие к рассчитанным величинам:

                                     R₂ = 430 кОм;   С₁ = 0,18 мкФ.

Аналогичным образом синтезируется электрическая схема регулятора скорости.

                                                                                                   18

4. СТАТИЧЕСКИЙ РАСЧЕТ САУ

После  синтеза регуляторов производят расчет САУ в установившемся режиме (статический расчет) с целью получения статической характеристики электропривода, расчета недостающих коэффициентов передачи, определения статической ошибки, диапазона регулирования и других технических показателей.

Этот расчет производят по уравнению привода в установившемся режиме, которое получают по его передаточным функциям при  р = 0. Рассмотрим, как это делается на примере расчета канала регулирования электродвигателя со стороны якоря За основу для расчета возьмем операторное уравнение канала якоря по частоте вращения в установившемся режиме:

                              ω = ФU (р) р=0 ⋅Uзад.с − Фм(р) р=0 ⋅ Мст ,              (4.1)

где ^Ф_U (р⁾ _р=0 = ^K_y ; Ф_м(р) _р=0 = K_м – коэффициенты передачи замкнутой САУ по управлению (U_зад) и возмущению (М_ст).

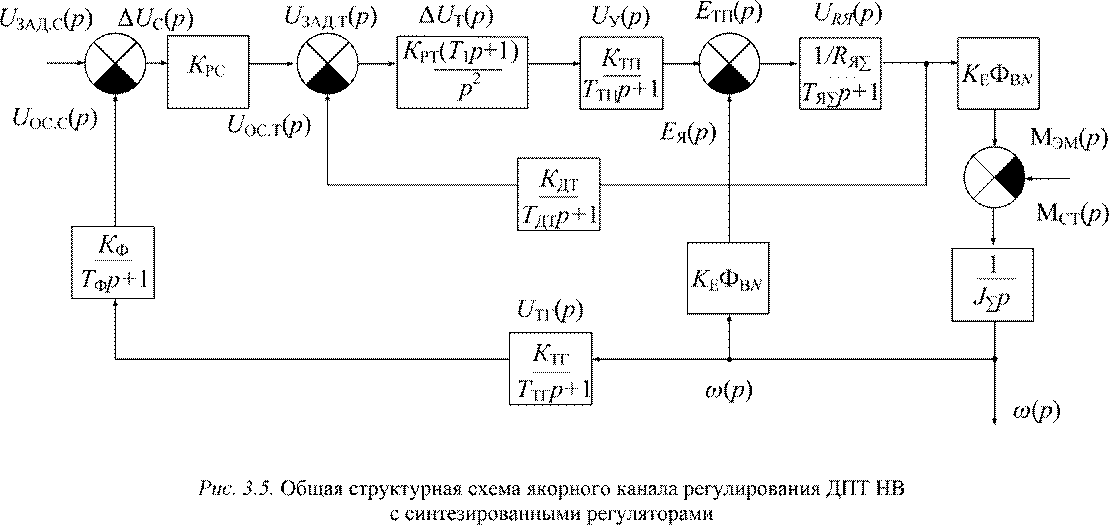
При определении коэффициентов передачи для изложенного выше примера по общей структурной схеме (рис. 3.5) с целью упрощения аналитических преобразований в исходной структурной схеме примем р = 0, кроме интегрирующих звеньев, и перейдем к расчетной схеме по рис. 4.1.

Используя структурные преобразования и приравнивая р = 0, как только это становится возможным, получим для  определения коэффициентов передачи по управлению и возмущению отдельные расчетные структурные схемы (рис. 4.2, 4.3).

По первой схеме с помощью правил структурных преобразований прир = 0 найдем коэффициент передачи САУ по управлению 

K_у = ω/U_зад.с = (K_ф · K_тг)^–1, что с учетом (2.6) дает уравнение статической характеристики управления на холостом ходу:

ωN ⋅Uзад.с.      (4.2)            ω =

^Uзад.с,N

                         По второй схеме аналогично можно получить

                                                                  Δω                  K_дт

                                  K_м =        =                                 ,

                                                                 Мст         Kрс ⋅ Kф ⋅ Knu ⋅ KеФвN

что с учетом п. 2.3 дает уравнение ошибки по скорости от момента нагрузки:

Uзад.т ⋅ωN

                                       Δω = ⋅ М_ст .                      (4.3)

Uзад.с ⋅ МN ⋅ Kрс

Объединяя (4.2) и (4.3) в соответствии с (4.1), запишем для рассмотренного случая уравнение механической характеристики САУ:

                                          ω = K_у ⋅U_зад.с − K_м ⋅ М_ст.                          (4.4)