Номинальные технические данные электродвигателя. Функциональная схема якорного канала двухзонной системы автоматического управления с подчиненными контурами регулирования токов якоря и возбуждения двигателя постоянного тока независимого возбуждения, страница 6

Если же ξ ≥1, то рассматриваемое звено является апериодическим 2-го порядка и оно может быть представлено двумя апериодическими звеньями 1-го порядка с передаточной функцией в виде:

TэмΣр/ RяΣ ,

(Т₁р +1)(Т₂ р +1)

где Т_1,2  = Т (ξ ±    ξ² −1) – новые постоянные времени.

В этом случае преобразованная структурная схема контура регулирования тока якоря (рис. 3.2) примет вид, представленный на  рис. 3.3.

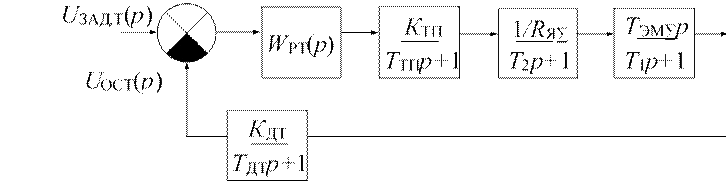
Рис. 3.3. Структурная схема контура регулирования тока якоря  к примеру синтеза регуляторов якорного канала

Обычно постоянные времени Т_тп, Т_дт, Т₂ являются малыми, поскольку Т₁ превышает их более, чем на порядок.

Тогда, следуя рекомендациям п. 2.5, запишем передаточную функцию регулятора тока как

K_рт(Т₁р +1)

                                            W_рт(р) = ₂ ,                           (3.3)

р

R^яΣ           – коэффициент передачи регулятора где K_рт =

Kтп ⋅ТэмΣ ⋅ Kдт ⋅2ТμΣ1

тока якоря, а Т_μ∑1 = Т_тп + Т_дт + Т₂ – суммарная малая постоянная времени контура регулирования тока якоря.

3.2. Синтез регулятора в контуре  регулирования скорости

Поскольку синтез регуляторов в САУ подчиненного регулирования ведется последовательно от внутреннего контура к внешнему, то с помощью правил преобразования структурных схем (Приложение 2) свернем контур регулирования тока якоря (рис. 3.3) до одного звена с учетом синтеза (3.3).

Передаточная функция прямого канала контура тока якоря:

1

                   Wкт.п(р) = .

2К_дт(Т_тп +Т_дт +Т₂ )р(Т_тпр +1)(Т₂ р +1)

Тогда передаточная функция замкнутого контура тока якоря:

(Т_дтр +1)/ К_дт

            Ф_кт(р) =  .

2(Т_тп +Т_дт +Т₂)р(Т_тпр +1)(Т₂ р +1)(Т_дтр +1) +1

С целью получения регулятора скорости, простого в реализации и удобного в настройке, упростим полученную передаточную функцию до апериодического звена 1-го порядка:

                                                                                 1/ Кдт                                 1/ Кдт

                                         Ф_кт(р) ≈     =      2(Ттп +Тдт +Т2 )р +1    2ТμΣ1 р +1

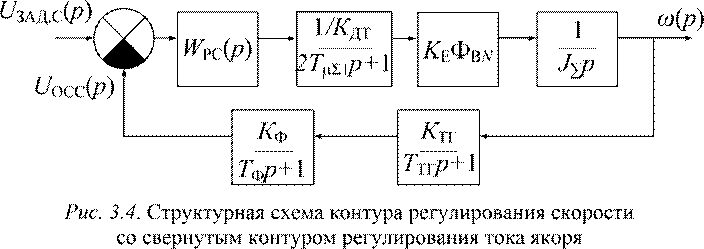
В этом случае структурная схема контура регулирования скорости принимает вид, показанный на рис. 3.4, и по рекомендациям п. 5 регулятор скорости будет иметь следующую передаточную функцию при условии, что все постоянные времени Т_ф, Т_тг, 2Т_μ∑1 являются малыми,

                                                                                           K^lnJ^Σ                    = K_рс,              (3.4)

                                              W_рс(р) = KeФвN ⋅ KтгKФ ⋅2ТμΣ2

где Т_м∑2 = Т_ф + Т_тг +  2Т_м∑1 – суммарная малая постоянная времени контура регулирования скорости; K_рс – коэффициент передачи регулятора скорости.

Обобщая результаты синтеза регуляторов (3.3) и (3.4), представим исходную схему канала (рис. 2.2) в конкретном виде (рис. 3.5).

Статическим и динамическим расчетом этой схемы в  дальнейшем проверяется правильность синтеза регуляторов.

3.3. Проектирование электрической схемы регулятора

Пусть для рассмотренного выше примера по заданию на проект и после анализа технического задания было получено:

 K_дт = 0,1 В/А; K_фK_тг = 0,08 Вс; K_тп = 20; R_я∑ = 0,8 Ом; Т_я∑ = 0,005 с;       Т_эм∑ = 0,05 с; Т_тп = 1 · 10^–3 с; Т_дт =  1 · 10^–3с.

Тогда для расчета передаточной функции регулятора тока якоря по выражению (3.3) дополнительно найдем согласно соотношений

(3.1) и (3.2):

                                            Т = 0,0158 с; ξ = 1,58.

Поскольку ξ > 1, то можно вычислить новые постоянные времени ДПТ НВ:

                                      Т₁ = 0,0443 с;   Т₂ = 0,0056 с.

Из полученного видно, что в контуре тока большая постоянная времени   Т₁ = 44,3 · 10^–3с, а суммарная малая постоянная времени 

                   Т_∑1 = Т_пт + Т_дт + Т₂ = (1 + 1 + 5,6) 10^–3 = 7,6 · 10^–3 с.

Передаточная функция регулятора  тока в соответствии с (3.3):