Номинальные технические данные электродвигателя постоянного тока независимого возбуждения. Каналы электродвигателя, в которых рассчитываются переходные процессы, страница 8

                    ⎨                                                               

^⎪⎪⎩d^dτω^о = 28.16¹⋅0.81[i_Я^о −[1−1(t)]⋅sign(ω^о)].

Определение функции sign sign(x) := if x(  0 ,0 ,if x( > 0 ,1 ,−1))

Определение функции-матрицы правых частей уравнений

                                           ⎡        28.16 ⋅ (1.0355 − y1) − y0           ⎤          -ток якоря

                                                                                    ⎢⎥                              y0

D t y( , ) :=-угловая скорость

                                                                                  ⎢⎤_⎦ ⎥                             y1

⎣⎦

Выберем интервал и шаг расчёта

                          τпп (5.. 10) ⋅ τэм        Δτ  0.5 ⋅ τв       N ^tпп

Δτ

Задание интервала и шага расчёта

t1 − t0

                     t0 := 0           t1 := 30        Δτ := 0.1       N  300

Δτ

Задание начальных условий

⎛1⎞ y := ⎜ ⎟

⎝1⎠

Расчёт

S := rkfixed y t0( ,  ,t1 ,N,D)

Перенос результатов в матрицы-столбцы

τ := S〈 〉0                 iя := S〈 〉1                       ω := S〈 〉2

                                                              о                                     о

Диаграммы изменения переменных (переходные процессы)

τ

Относительное время

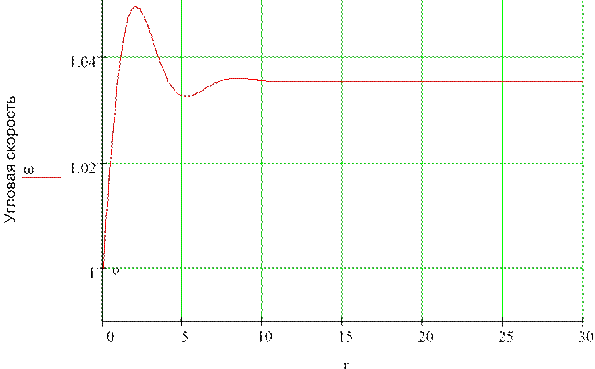
Относительное время

                Рис. 3.1. Переходные процессы по току якоря и угловой скорости

3.3 Пример анализа полученных результатов расчета  переходных процессов.

Целью анализа рассчитанных переходных процессов является определение ихсоответствие физическим процессам происходящим в ДПТ НВ.

При анализе рассматриваются три основных момента: начало,установившееся значение и характер переходного процесса.

Исходное(начало) и новое(установившийся режим) состояние ДПТ

НВ наиболее просто установить аналитически по законам Кирхгофа, Ампера и Фарадея, которые для установившихся режимов аналитически описываются  согластно (2.1) и (2.2)  следующими уранениями

⎧U_Я = I_Я ⋅ R_Я + E_Я ,

⎪

UВ = IВ ⋅ RB,

⎪

⎪

                         ⎨МЭМ = МСТ ⋅sign(ω),                 

⎪EЯ = КE ⋅ КФN ⋅WB ⋅ IВ ⋅ω, ⎪

⎪⎩MЭМ = КE ⋅ КФN ⋅WB ⋅ IВ ⋅ IЯ.

В относительных величинах  они примут вид

                                ⎧ о                      iо

⎪uЯ =о + eЯ ,

⎪Я

⎪uВо = iBo,

                               ⎪    ^{о                   о                          о}

                  ⎨М_ЭМ = М_СТ ⋅sign(ω ),                                                                             (3.3)

                                ⎪ о             o          o

_⎪e_Я = i_B ⋅ω ,

                               ⎪M_ЭМо  = i_Bo ⋅i_Яо .

⎪

⎩

Проведем анализ переходных процессов, полученных в п.3.2.

В момент времени t = 0₋перед сбросом нагрузки все величины были равны номинальным значениям:

UЯ =UЯN ,UB =UBN ,MCT = MЭМ = MN ,

iЯ = iЯN ,iB = iBN ,ω=ωN.

В относительных величинах получим при t = 0₋:

                                                     U^ЯN                                               U^BN                                                            M ^N

                                        u_Я ° = =1.0355,u_B° = =1,M_CT ° = M_ЭМ ° = =1,

                                                     EЯN                                               UBN                                                             M

                                                                                                                                                         _N             

I     I           ω i_Я ° = ^ЯN =1,i_B° = ^BN =1,ω° =  ^N =1.

                                                    IЯN                              IBN                            ωN

В момент времени t = 0₊сразу после сброса нагрузки эти величины, в соответствии с законами коммутации, будут равны

u_Я ° =1.0355,u_B° =1,M_CT ° = 0,

i_Я ° =1,i_B° =1,ω° =1.