Номинальные технические данные электродвигателя постоянного тока независимого возбуждения. Каналы электродвигателя, в которых рассчитываются переходные процессы, страница 4

                                       ⎪                                        dω

                                         ⎪⎩К_E ⋅ К_ФN ⋅W_B ⋅i_B ⋅i_Я = J_Я ^⋅ _dt + M_СТ ⋅ sign(ω).     

Система уравнений (2.3)         достаточна, так как она имеет три уравнения для трёх неизвестных (i_Я , i_B ,ω).

             Решим её относительно первых производных этих неизвестных

                                        ⎧di_Я              1             R_Я                     КE ⋅ КФN ⋅WB                                                    

                                       ⎪       =       ⋅u_Я −       ⋅iЯ −                      ⋅iB ⋅ω,

                                        ⎪ dt       L_Я                     L_Я                                   L_Я                                           

                                       ^⎪⎪di_В            1             R_В                                                                                      

                                          ⎨ dt = L_В ⋅uВ −   ⋅iВ,                                                              (2.4)

                                       ⎪                       LВ

                                           ⎪dω КE ⋅ КФN ⋅WB                                   1                              

                                       ⎪      =                      ⋅i_B ⋅i_Я −  ⋅ M_СТ ⋅ sign(ω).   

                                       ⎪⎩ dt               J_Я                                           iЯ                                                   

При введении относительных величин рекомендуется в качестве базовых выбирать номинальные паспортные значения электродвигателя

(табл. 1.1) так, чтобы 

i^Я u^Я ω i^В u^В М^СТ t                   i_Я ° = ,u_Я ° = ,ω° = ,i_В° = ,u_В° = ,М_СТ ° = ,τ= .

                                        IЯN                        EЯN                    ωN                      IВN                       UВN                              МN          TЯ

Здесь верхний индекс «0» означает, что переменная представлена в относительных единицах, а нижний «N» указывает на номинальное значение переменной.

Относительное время τ определено через базовую величину, равную электромагнитной постоянной времени якорной цепи

LЯ

                                                         T_Я =      .

R_Я

Запишем систему уравнений (2.4) через относительные переменные, использую указанные рекомендации.

Технику выполнения преобразований покажем на примере первого уравнения

IЯN ⋅iЯ

− RЯ ⋅ IЯN ⋅iЯ − КE ⋅ КФN ⋅WB ⋅ IВN ⋅iВ ⋅ωN ⋅ω;

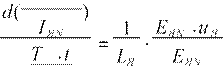             d( Я         )                                 LЯ            IЯN                             LЯ                          IВN                ωN

T^Я

iЯ

           IЯN ⋅d(IЯN )       EЯN            Я                                                                                                                           i        ω

                                                                     − RЯ ⋅ IЯN ⋅ iЯ − КE ⋅ КФN ⋅WB ⋅ IВN ⋅ωN ⋅ В ⋅           .

                                                                        LЯ              IЯN                                     LЯ                                     IВN ωN

           ^T_Я ⋅d(      )

T_Я

Освобождаясь от коэффициентов при производной и используя обозначения относительных переменных, получим

                   diЯ °     EЯN ⋅TЯ                         RЯ ⋅TЯ                          КE ⋅ КФN ⋅WB ⋅ IВN ⋅ωN ⋅TЯ

                    =             ⋅uЯ ° −           ⋅iЯ ° − iB°⋅ω°.

                         dτ LЯ ⋅ IЯN                                  LЯ                                                      LЯ ⋅ IЯN

Действуя аналогично, запишемдва другихуравнения системы (2.4) через относительные переменные в виде

                       diВ°     UЯN ⋅TЯ                        RВ ⋅TЯ