Структура кристаллов. Кристаллическая решетка. Индексы Миллера. Плотность упаковки. Координационное число, страница 5

3.3  Модель Дебая для теплоемкости

По этой модели частицы в узлах кристаллической решетки, так же как и в модели Эйнштейна, представляет собой квантовые гармонические осцилляторы. Однако, в отличие от модели Эйнштейна они являются зависимыми (связанными). В связи с этим полная внутренняя энергия системы зависимых осцилляторов можно было представить как сумма энергий отдельных осцилляторов. По аналогии с моделью Эйнштейна средняя энергия осциллятора имеет следующий вид: 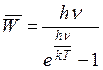. Полная внутренняя энергия  может быть представлена в следующем ви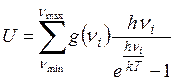де: , где  – число колебаний с n_i частотой, n_max, n_min – max и min частоты осцилляторов.

Нахождение этой суммы представляет чисто математические трудности. Поэтому для нахождения указанной суммы Дебай пошел на 2 упрощений:

1)  Дебай заменил дискретную среду непрерывной (появилась сферическая симметрия).

2)  Пренебрег различиями продольных и поперечных колебаний.

С учетом этих допущений g(n) можно представить в виде , где А – const. Сумма может быть заменена интегралом:

.

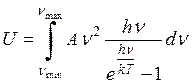Так как число колебаний с min частотами стремится к 0, то нижний предел интегрирования может быть заменен 0. 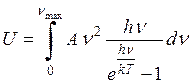. В итоге имеем уравнение для полной энергии с 2-мя неизвестными A и n_max. Для нахождения этих неизвестных и решения этих уравнений Дебай учел 2 обстоятельства:

1)  Общее число колебаний должно быть равным 3N.

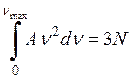
2)  В области высоких температур полная внутренняя энергия должна быть равна 3RT, то есть соответствовать классическому закону.

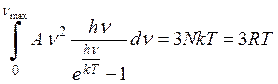
Получим 2 уравнения для нахождения 2-х неизвестных. Выразив из этих уравнений неизвестные  то, полная внутренняя энергия системы представится в следующем виде:

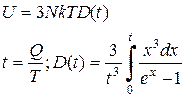. Проанализируем это выражение для полной внутренней энергии.

Рассмотрим 2 интервала температур:

1)  T®¥.

 

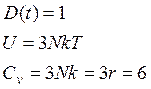
В области высоких температур модель Дебая дает нам классический результат.

2)  T®0.

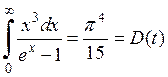
подставим такое значение  интеграла в выражение для полной энергии U, получим:

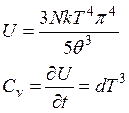
Мы видим, что в области низких температур в модели Дебая теплоемкость стремится к 0, но, в отличие от модели Эйнштейна, по закону T³, что соответствует экспериментальным данным. В области низких температур модель Дебая более четкая и справедливая, чем модель Эйнштейна. Такое положение справедливо для простейших кристаллических структур. С усложнением решетки колебания частиц в большей степени описывается верхней ветвью закона дисперсии (оптическая ветвь). В связи с этим такие колебания лучше могут быть описаны моделью Эйнштейна.

Структурные дефекты и их классификация.

Структурные дефекты – это энергетически  возбужденное состояние кристаллической решетки, предполагающее изменение способа заполнения узлов решетки. Образуются как во время роста кристалла, так и при изменении состава окружающей среды (Р, Т, состав газовой фазы и т. д.).

Виды классификаций:

1)Макроскопические и микроскопические дефекты.

Макроскопические (трещины, царапины, включение другой фазы) – по величине значительно превосходят

2) Равновесные и неравновесные.

Равновесные дефекты – снижают свободную энергию кристалла до их определенной концентрации.

3) По геометрическому признаку кристаллы делятся на:

а) точечные (нульмерные) б) линейные (дислокации)

в) поверхностные (двумерные)

г) объемные (трехмерные)

Точечные дефекты.

1) Замена «свой чужой»

АВАВАВ

ВАААВА

2) Вакансии (дефект по Шотке) – удаление частицы из узла без изменения поверхностной энергии кристалла. Место куда попадает частица это край дислокации.

Вакансия является непарным дефектом, но для иных кристаллов возникают парами.

3) Дефекты по Френкелю – парный представляет собой вакансию + атом в междоузлии.

 

- вакансия

  - междоузельный атом