2) Рассмотрим верхнюю ветвь колебаний. x = -h, так как колебания легких и тяжелых частиц происходят в противофазе, при чем, центр масс не меняет своего положения. Качественно это можно представить следующим образом:
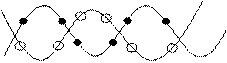 |
Такие закономерности колебаний присуще колебаниям оптического диапазона. Поэтому верхняя ветвь называется оптической.
Таким образом, для цепочки атомов 2-х сортов мы получили закон дисперсии в виде 2-х ветвей (оптической и акустической). Частота оптических колебаний слабо зависят от квазиволнового числа к, а для акустической ветви эта зависимость более сильная. Естественно предположить, что с умножением модели, с точки зрения количества атомов и обобщение на 3-х мерный случай, спектр колебания также будет представлять набор ветвей колебаний (часть акустических, часть оптических). В частности будут существовать продольные и поперечные акустические и оптические ветви. То есть спектр колебания реальных материалов в принципе также может быть представлен в виде ветвей колебаний, что соответствует экспериментальным данным.
Рассмотрим цепочку одинаковых атомов. Будем считать,
что цепочка содержит N атомов. Воспользуемся классическим
законом равномерного распределения энергии по степеням свободы. (на 1 степень
свободы приходится ![]() ). И
учтя, что цепочка атомов обладает 2N степенями свободы, мы
можем определить полную внутреннюю энергию цепочки одинаковых атомов:
). И
учтя, что цепочка атомов обладает 2N степенями свободы, мы
можем определить полную внутреннюю энергию цепочки одинаковых атомов: 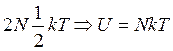 . Отсюда
теплоемкость:
. Отсюда
теплоемкость: 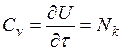 .
.
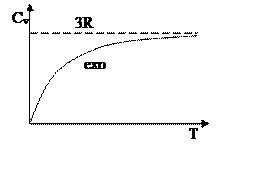
Обобщив на 3-х мерный случай, получим: 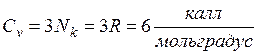 – суть закона
Дюлонга и Пти. Теплоемкость есть величина постоянная, не зависящая от
температуры. Если рассмотреть реальные эксперименты, зависимость теплоемкости
от температур, она не будет величиной постоянной: В области низких температур
она стремится к 0, а в области высоких температур она стремится к постоянному
значению.
– суть закона
Дюлонга и Пти. Теплоемкость есть величина постоянная, не зависящая от
температуры. Если рассмотреть реальные эксперименты, зависимость теплоемкости
от температур, она не будет величиной постоянной: В области низких температур
она стремится к 0, а в области высоких температур она стремится к постоянному
значению.
Классический закон Дюлонга и Пти выполняется
в области высоких температур.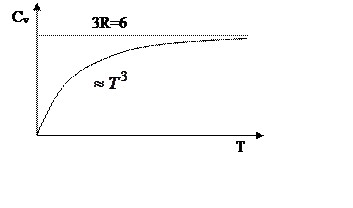 Для объяснения поведения теплоемкости в области низких температур, получим, что
пользоваться классическими представлениями нельзя, так как они являются слишком
грубыми. В связи с этим необходимо учесть квантово – механический характер
поведения частиц в материалах.
Для объяснения поведения теплоемкости в области низких температур, получим, что
пользоваться классическими представлениями нельзя, так как они являются слишком
грубыми. В связи с этим необходимо учесть квантово – механический характер
поведения частиц в материалах.
По модели Эйнштейна частицы в узлах
кристаллической решетки моделируются в виде гармоничных квантовых
невзаимодействующих осцилляторов. Энергия каждого осциллятора является
величиной квантовой, то есть можем представить ![]() , где w – круговая
частота, n – целое число.
, где w – круговая
частота, n – целое число.
Найдем среднею энергию осциллятора. Для этого воспользуемся формулой Больцмана:
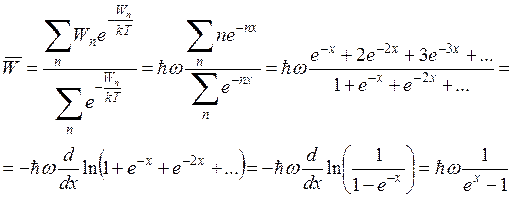
![]()
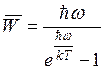 –
средняя энергия осциллятора.
–
средняя энергия осциллятора.
Найдем полную внутреннюю энергию системы и
проанализируем ее для разных интервалов температур: ![]() .
.
1) T®¥ (для области высоких температур):

![]() – средняя энергия осциллятора в области высоких температур.
– средняя энергия осциллятора в области высоких температур.
![]() – полная энергия осциллятора в области высоких температур.
– полная энергия осциллятора в области высоких температур.
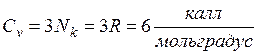 .
.
2) Проанализируем область низких температур:
T®0. ![]() ,
, ![]() ,
, 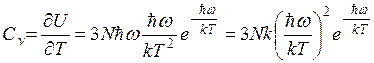 . Поучим, что Сv уменьшается в области низких температур.
. Поучим, что Сv уменьшается в области низких температур.
 При
чем уменьшается по экспоненциальному закону. А эксперимент дает T3. Модель Эйнштейна имеет определенные
недостатки. Следует отметить, что дискретный характер колебаний частиц, когда Cv®0 в области низких температур,
имеет место для тех значений теплоемкости, когда T=0. При
некоторых температурах, называемых характеристическими температурами
Эйнштейна, дискретность спектра колебаний перестает сказываться и можно
пользоваться классическими представлениями (то есть з. Дюлонга и Пти). Эту
характеристическую температуру Эйнштейна можно ввести следующим образом:
При
чем уменьшается по экспоненциальному закону. А эксперимент дает T3. Модель Эйнштейна имеет определенные
недостатки. Следует отметить, что дискретный характер колебаний частиц, когда Cv®0 в области низких температур,
имеет место для тех значений теплоемкости, когда T=0. При
некоторых температурах, называемых характеристическими температурами
Эйнштейна, дискретность спектра колебаний перестает сказываться и можно
пользоваться классическими представлениями (то есть з. Дюлонга и Пти). Эту
характеристическую температуру Эйнштейна можно ввести следующим образом: ![]() . Тогда средняя
энергия осциллятора с учетом температуры Эйнштейна:
. Тогда средняя
энергия осциллятора с учетом температуры Эйнштейна: 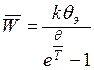 .
.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.