Кристаллическую структуру принято описывать с помощью периодически повторяющейся в пространстве элементарной части кристаллической решетки, которая называется элементарной ячейкой (элементарным параллелепипедом), с каждой точкой которой связана некоторая группа атомов. Эта группа атомов называется базисом; базис повторяется в пространстве и образует кристаллическую структуру.
Кристаллическая решетка есть пространственная сетка, в углах которой расположены частицы (атомы, ионы, молекулы в зависимости от типа химической связи).
Основным свойством кристаллической решетки
является трансляционная симметрия, т. е. при смещении решетки на вектор![]() решетка
совмещается сама собой.
решетка
совмещается сама собой.
Здесь
![]() –
целые числа;
–
целые числа; ![]() –
базисные вектора трансляций. (Они равны периодам решетки по соответствующим
координатам).
–
базисные вектора трансляций. (Они равны периодам решетки по соответствующим
координатам).
Операцию перемещения кристалла как целого параллельно самому себе, описываемую вектором r, называют трансляцией.
Движением кристалла называется операция, совершаемая над кристаллом, при котором расстояние между любыми двумя точками данного кристалла остаются неизменными.
Простейшие движения: повороты вокруг некоторой оси n-го порядка, зеркальное отражение, инверсия – движение, в результате которого координаты тела меняют свой знак относительно центра инверсии.
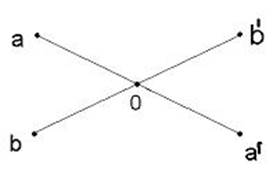
О – центр инверсии, при движении относительно которого точки А и В переходят соответственно в А и В.
Движение, в результате которых фигура или тело совмещается сама с собой, называется элементами симметрии данного тела или фигуры.
Совокупность элементов симметрии для данного тела называют группой симметрии.
В связи с этим элементарную ячейку выбирают таким образом, чтобы она обладала максимальным числом элементов симметрии и характеризовала собой группу симметрии тела или решетки в целом.
Группы типа Сn: элементами симметрии для таких групп будут
повороты тела вокруг оси n-го порядка на угол ![]() . Для кристалла
характерны группы типа: С1, С2, С3, С4,
С6. Оси пятого порядка в кристаллах не существует!
. Для кристалла
характерны группы типа: С1, С2, С3, С4,
С6. Оси пятого порядка в кристаллах не существует!
Группы типа Sn: элементами симметрии для таких групп
являются повороты вокруг некоторой оси n-го порядка Сn
и отражения в плоскостиsh,
перпендикулярной данной оси. ![]()
Группы типа Сnv:
сочетание поворота вокруг оси n-го порядка Сn и отражение в плоскости, проходящей через данную ось sv. ![]() .
.
Если к точечным группам симметрии добавить трансляционную симметрию, то получим пространственные группы симметрии. Всего их 230 .
 Индексы Миллера являются общепринятым способом
обозначения узлов, направлений и плоскостей в кристалле.
Индексы Миллера являются общепринятым способом
обозначения узлов, направлений и плоскостей в кристалле.
x=ma, y=nb, z=pc,
где a,b,c – параметры решетки, m,p,n – целые числа.
[[m,p,n]] – индексы Миллера для узла.
2. Индексы направления. Для описания направления в кристалле выбирается прямая, проходящая через начало координат. Ее положение однозначно определяется индексами [[m,p,n]] первого узла, через который она проходит. Поэтому индексы узла [[m,p,n]] являются одновременно индексами направления и обозначаются [m,p,n].
3. Индексы плоскости определяются следующим образом.
1) Берут отрезки, отсекаемые плоскостью на осях координат.
2)
Берут величины, обратные этим отрезкам: 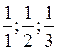 .
.
3)
Приводят к общему знаменателю: 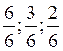 .
.
4) Отбрасывают знаменатель. (6,3,2) – индексы Миллера для плоскости.
Если плоскость параллельна какой – либо оси, ее проекция на эту ось равна ¥. Для такой плоскости соответствующий индекс Миллера равен нулю. Если плоскость отсекает некоторый отрезок с отрицательным знаком, то соответствующий индекс Миллера, будет также отрицательным (черточка ставится сверху над индексами).
Пример:
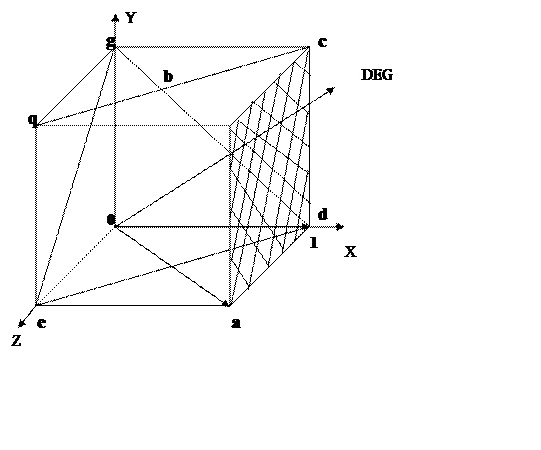
Пусть длина ребра куба равна параметру решетки а.
1) Тогда плоскость abcd будет иметь индексы Миллера (1 0 0).
Если мы хотим обозначить не одну плоскость, а семейство всех граней куба, то индексы Миллера пишутся в фигурных скобках {100}.
2) Плоскость cdeq будет иметь индексы Миллера (1 0 1).
3) Плоскость 1eq будет иметь индексы Миллера (1 1 1).
Индексы Миллера для направлений в отличие от индексов Миллера для плоскостей помещаются не в круглые скобки, а в квадратные скобки.
Для простой кубической решетки (см. рис. 1):
Направление ОХ имеет индексы Миллера [1 0 0]
Направление ОА имеет индексы Миллера [101].
Направление, перпендикулярное какой-либо плоскости, имеет те же индексы Миллера, что и плоскость.
Смоделируем частицы в узлах кристаллической решетки в виде идеальных (не деформированных) соприкасающихся шаров. Тогда плотность упаковки данной решетки представляет собой отношение объема шаров, попадающих внутрь элементарной ячейки, к объему всей ячейки.
Пример: Рассмотрим простую кубическую решетку.
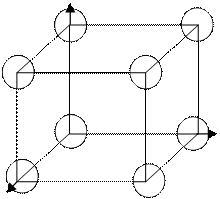 Пусть
радиус шара r. Объем одного шарика
Пусть
радиус шара r. Объем одного шарика ![]() . В ячейке часть
шарика
. В ячейке часть
шарика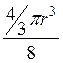 . В ячейке часть
всех шариков. Тогда плотность упаковки:
. В ячейке часть
всех шариков. Тогда плотность упаковки: 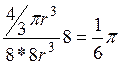 .
.
Координационное число – число ближайших соседей данной частицы в решетке. В зависимости от внешних факторов плотность упаковки, соответственно и координационное число могут меняться. Это приводит к тому, что данный материал может существовать в различных кристаллических модификациях (полиморфизм).
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.