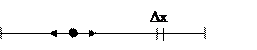 Пусть
совершаются продольные колебания. Выделим элемент струны Dx. Рассмотрим силы,
приложенные к этому элементу, и найдем его смещение U.
Тогда деформация струны
Пусть
совершаются продольные колебания. Выделим элемент струны Dx. Рассмотрим силы,
приложенные к этому элементу, и найдем его смещение U.
Тогда деформация струны 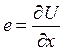 ,а
силовая постоянная
,а
силовая постоянная 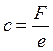 .
.
Пусть линейная плотность струны r. Тогда на выделенный элемент будут действовать две силы:
![]()
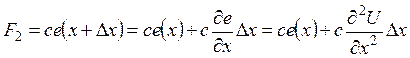
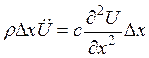
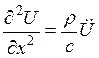
![]()
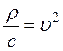 –
скорость распространения колебания в материале.
–
скорость распространения колебания в материале.
![]() (закон
дисперсии), где
(закон
дисперсии), где 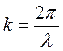 -
квазиволновое число
-
квазиволновое число
 |
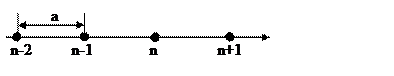 |
Будем считать, что каждый атом
взаимодействует лишь с ближайшими соседями как наиболее сильное влияние
оказываемое. Влияние более удаленных атомов будем пренебрегать. Рассмотрим силы
действующие на n-й атом. Исходя из предположения о
взаимодействии с ближайшими соседями мы можем представить что силы действующие
на n-й атом можно представить в виде: ![]() .
.
Где – b – упругая const;
Un – смещение n-го атома;
Un-1 – смещение (n-1)-го атома.
Замечание 1: связь упругой и силовой постоянных.
Рассмотрим смещение упругой цепочки.
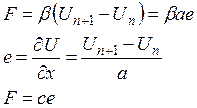
![]() – связь упругой и силовой const.
– связь упругой и силовой const.
Зная выражение для силы запишем закон
движенияn-го атома: – уравнение движения n-го атома: ![]() –
уравнение движение n-го атома.
–
уравнение движение n-го атома.
Решение этих уравнений будем искать в виде:![]()
Подставим решение в уравнение движения n-го атома. Имеем:
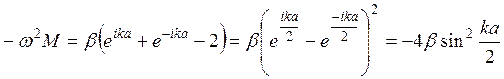
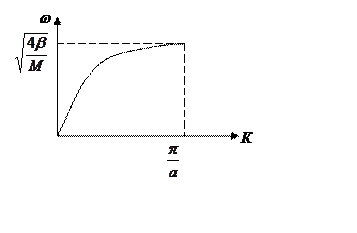
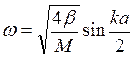 , –
закон дисперсии.
, –
закон дисперсии. 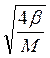 –
амплитуда колебаний.
–
амплитуда колебаний. 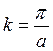 . Этому
соответствует экстремальному значению.
. Этому
соответствует экстремальному значению.
Значение к в интервале от 0 до ![]() дает все возможные
значения спектра колебания цепочки одинаковых атомов. Все другие колебания, вне
этого интервала, фактически повторяют колебания в первой четверти волны. Для
расчета этого спектра достаточно 1-й четверти волны. Следовательно, отметим,
что в зависимости от к, наш закон дисперсии, также может быть изменен.
Фактически при к→0, w→0 спектр колебаний цепочки атомов соответствует спектру колебаний
струны (при к→0).
дает все возможные
значения спектра колебания цепочки одинаковых атомов. Все другие колебания, вне
этого интервала, фактически повторяют колебания в первой четверти волны. Для
расчета этого спектра достаточно 1-й четверти волны. Следовательно, отметим,
что в зависимости от к, наш закон дисперсии, также может быть изменен.
Фактически при к→0, w→0 спектр колебаний цепочки атомов соответствует спектру колебаний
струны (при к→0).
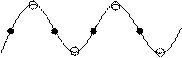
Предположим, что имеем цепочку атомов с легкой массой m и тяжелых с массой M. Расстояние между атомами – a.
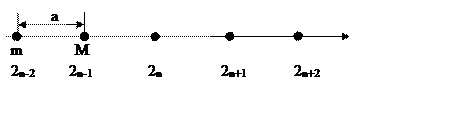 |
Пусть легкие занимают четные положение, а тяжелые – нечетные. Рассмотрим колебание таких разнородных атомов. С этой целью запишем законы движения для легких и тяжелых частиц. Учтем влияние лишь ближайших соседей на движение данного атома. Влиянием более удаленных частиц будем пренебрегать.
![]() Для легких частиц:
Для легких частиц: ![]()
Для тяжелых частиц: ![]()
Решение этой системы уравнений будем искать в следующем виде:
![]() – для легких атомов.
– для легких атомов.
![]() – для тяжелых атомов.
– для тяжелых атомов.
Подставим такие решения в уравнение движения получим систему линейных однородных уравнений относительно x и h. Система линейных однородных уравнений будет иметь ненулевое решение в том случае если определитель равен нулю.
(реш. Систему этих уравнений).
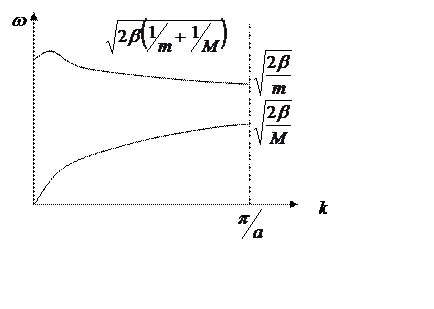 |
Проанализируем эти ветви (найдем физический смысл):
В уравнениях описываемых движение легких и тяжелых атомов и – есть амплитуды колебаний частиц.
1)
 |
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.