Информатика и выч. техника \ Проектирование информационных систем

Количественные характеристики надежности восстанавливаемых систем, два параллельных элемента, нагруженный резерв

Страницы работы

Уважаемые коллеги! Предлагаем вам разработку программного обеспечения под ключ.

Опытные программисты сделают для вас мобильное приложение, нейронную сеть, систему искусственного интеллекта, SaaS-сервис, производственную систему, внедрят или разработают ERP/CRM, запустят стартап.

Сферы - промышленность, ритейл, производственные компании, стартапы, финансы и другие направления.

Языки программирования: Java, PHP, Ruby, C++, .NET, Python, Go, Kotlin, Swift, React Native, Flutter и многие другие.

Всегда на связи. Соблюдаем сроки. Предложим адекватную конкурентную цену.

Заходите к нам на сайт и пишите, с удовольствием вам во всем поможем.

Содержание работы

Вопрос 5. Количественные характеристики надежности восстанавливаемых систем, два параллельных элемента, нагруженный резерв (стр. 421)

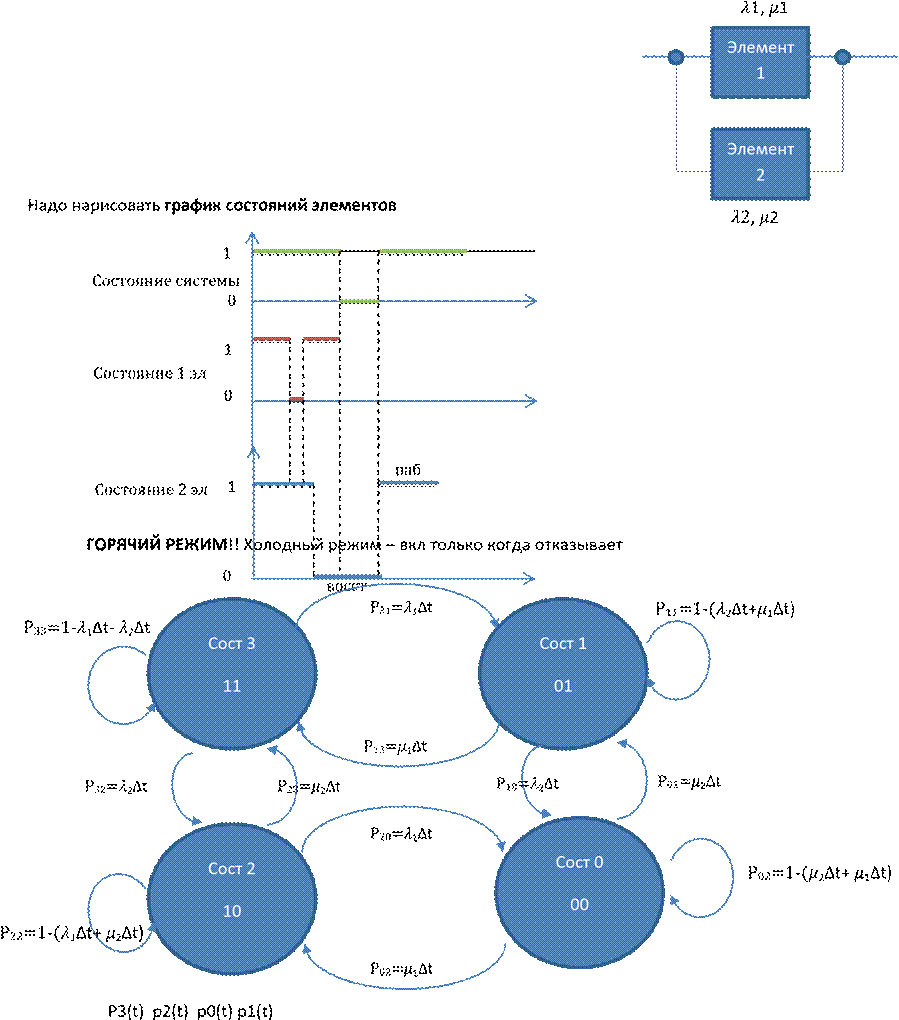Найти: функцию готовности и коэффициент готовности.

В случае, когда оба элемента находятся в горячем режиме, отказы могут быть как у основного, так и у резервного. Предположим, что потоки отказов Пуассоновские, также предположим, что система с восстановлением, поглощающего состояния нет. Также предположим, что интенсивности отказов и восстановления разные.

или

Найдем вероятности переходов.

Сделаем предположение за ∆t не могут оба восст - поглащаемое…

Для решения сделаем таблицу состояний

*Состояние*	*Состояние*	*Состояние*	*Описание*
*Элемент 2*	*Элемент 1*	*системы*
1	1	3	Оба эл раб, сист работает
1	0	1	Один эл отказал
0	1	2	Элемент 2 отказал, 1 работает – система работает
0	0	0	Элементы 1,2 отказали - Система восстанавливается

Рассмотрим (t, t+∆t) где ∆t достаточно маленький интервал.

Вероятность того, что Система находится в состоянии p₀, p₁, p₂, p₃ (стр 423)

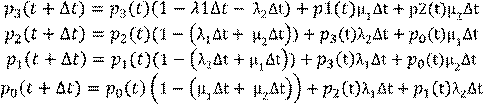
Разделим на ∆t и получим систему дифф уравнений Колмогорова

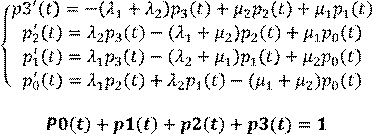
Свести к системе линейных уравнений переходя от оригиналов к изображению, используя теорию операционного счисления.

Предположим (начальные условия)

Метод решения стандартный, переходим к системе линейных уравнений. От оригиналов к изображениям используя формулу операционного счисления (берем от p0(t) интеграл)

P₀(t)→p₀(s) … P’₀(t)→sp₀(s) - ~~p0(0)~~

P₁’(t)→ sp₁(s) – 0

P₂’(t)→ sp₂(s) – 0

P₃’(t)→ sp₃(s) – p₃(0)= sp₃(s) – 1

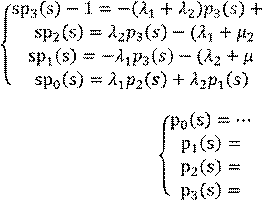
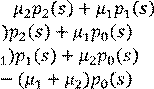Система линейных уравнений относительно p0, p1,p2,p3 переходим к оригиналам (берем интеграл) – обратное преобразование Лапласа

… ищем в таблице похожее и переходим к

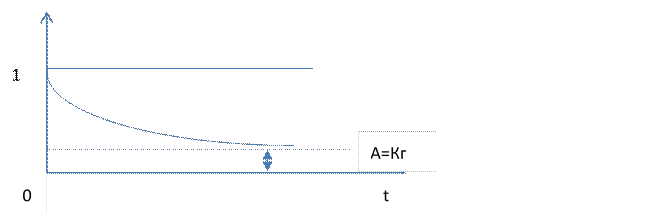
Функция готовности по теореме о вероятности противоположного события

Вопрос: задаем надежность КТС либо как коэффициент готовности – предельное значение, когда t к

∞ , либо функцию готовности - вероятность (функция – 5000 часов – не ниже)

Когда N элементов параллельно

Для каждого элемента задано и t – перемножаем полученные надежности, получаем коэффициент готовности; результат: если меньше заданного числа, надо резервировать (где самая маленькая надежность), если больше, все ОК.