Вопрос 4. Количественные характеристики надежности восстанавливаемых систем, один элемент
Задача о запасных элементах
 Пусть система состоит
из 1 элемента
Пусть система состоит
из 1 элемента
Запасных элементов n
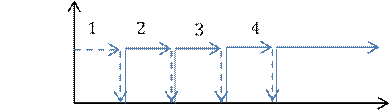
3 элемента в запасе, 3 хватит на время t?
Найти вероятность того, что число отказов ≤ N
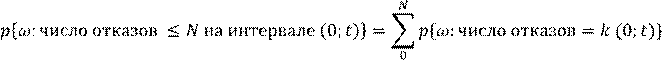
По условию поток простейший, значит, используем формулу Пуассона
![]()
( )
∑
{ ( )} ∑![]()
![]() ( )
( )
( )
( )
( ) ( )
( ) ( ) { ⏟ } ( )
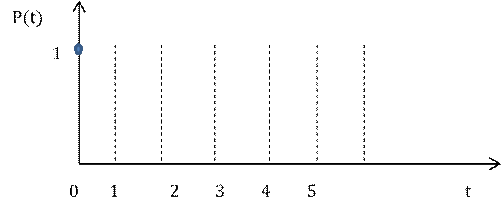
Построим график вероятности P(t) когда ![]() =2 (1/час),
N=6, T=5 часов
=2 (1/час),
N=6, T=5 часов
![]()
![]()
![]()
![]()
![]()
![]() С
вероятностью.. хватит 2 часа
С
вероятностью.. хватит 2 часа
![]()
![]()
![]() - загрузка рем бригада ,
- загрузка рем бригада , ![]()
нет времени!!!!
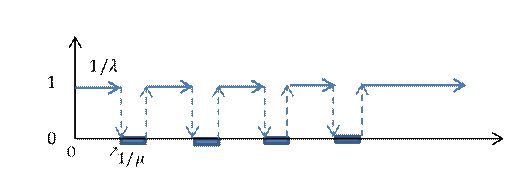
Ищем функцию готовности (g(t)) – система в рабочем состоянии
Перечислим все возможные состояния в котором может находиться система
|
Состояние элемента |
Состояние системы |
Описание |
|
1 (работает) |
1 |
Элемент работает, система работает |
|
0 (отказ) |
0 |
Элемент отказал, система отказала, идет восстановление |
Нарисуем граф состояний
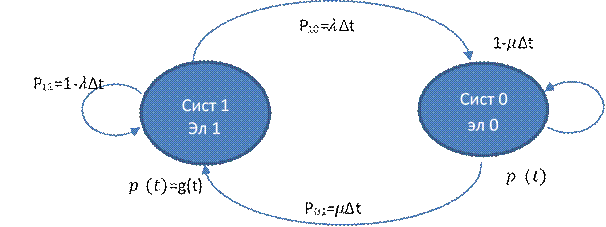
Возьмем маленький промежуток времени ∆t, G(t) - формула готовности, по формуле пуассона см выше
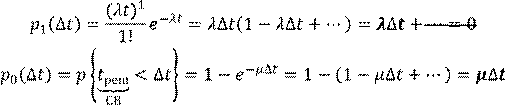
напишем уравнение равновесия (Колмогорова) для каждого состояния
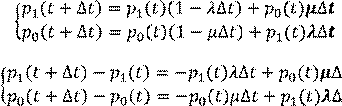
![]() P(A)=p(A/Bi)p(Bi)+.. по формуле
полной вероятности
P(A)=p(A/Bi)p(Bi)+.. по формуле
полной вероятности
Делим на ∆t и к ∞
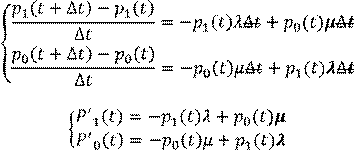
Получили систему диф уравнений с двумя неизвестными. Существует стандарный метод решения p0(0)=0, p1(0)=1 (в нуле никогда не отказывает и всегда работает)
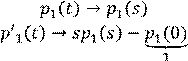
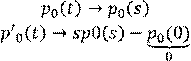
Перешли к линейным уравнениям
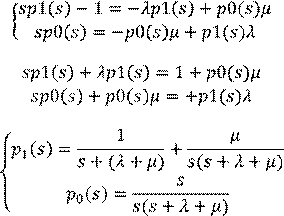
![]()
![]()
![]()
 Корн, Корн справочник
по математике - раздел – «операционное счисление» → по нему переход к оригиналу
(через интеграл)
Корн, Корн справочник
по математике - раздел – «операционное счисление» → по нему переход к оригиналу
(через интеграл)

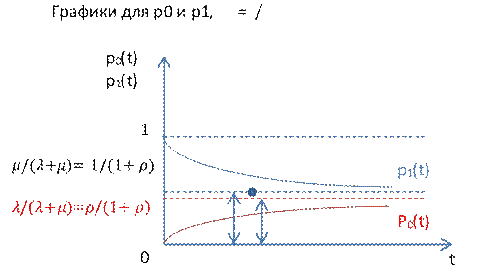
Замечание 1. P1(t)-функция готовности g(t) –
это показатель надежности работы. При t к беск, t стремится к асимптотич
значению ![]() /(
/(![]() +
+![]() )-коэффициент готовности
)-коэффициент готовности
![]()
Предельное (стационарное) значение при t → ∞
![]()
Задаем требование по надежности или функция готовности, значение должно быть выше точки
Сравним систему без восстановления с системой с восстановлениями
• Старое - Без восст
![]()
• восстанавливающиеся
o
μ→∞ ![]()
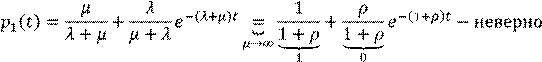
o μ→0 должны получить формулу без восст (частный случай- система без восст)
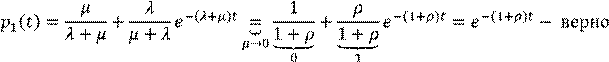
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.