Цели и задачи технико-экономических расчетов в энергетике, особенности их выполнения. Инструкция по определению экономической эффективности капитальных вложений в развитие энергетического хозяйства в качестве показателя, страница 4

Цифры, стоящие в клетках таблицы, характеризуют затраты на транспортировку 1 ту.т.  от источника к потребителю. Принять, что стоимость 1 ту.т. на первой базе составляет 20 р., на второй – 15 р.

Требуется определить оптимальный план топливоснабжения и замыкающие затраты на топливо у потребителей.

Решение.     Сформулированная выше задача относится к классу транспортных задач линейного программирования и поэтому может быть решена с помощью соответствующих методов, например, с помощью метода потенциалов.

Поскольку при определении оптимального варианта топливоснабжения следует учесть не только затраты не перевозку, но и затраты на добычу топлива, то переформируем исходную матрицу, представленную в табл. 1, учтя в ней, помимо транспортных расходов, также стоимость топлива (табл. 2).

                                                                                                                 Таблица 2

На первом этапе решения следует, прежде всего, определить исходное допустимое базисное решение. Для этого воспользуемся диагональным методом. Строим табл. 3, в которую вводим дополнительный фиктивный пункт потребления, так как мощность баз превышает потребность (открытая транспортная задача)

                                                                                                                        Таблица 3

В соответствии с процедурой диагонального метода строим серию таблиц, заполняя каждую из них, начиная с первой. В результате получим исходное базисное решение: Х₁₁ = 60; Х₁₂ = 45; Х₁₃ = 80; Х₁₄ = 70; Х₁₅ = 45; Х₂₅ = 10; Х₂₆ = 140.

Далее составляем для базисных переменных уравнения

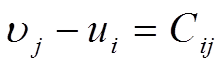
х₁ – u₁ = 22; х₂ – u₁ = 23; х₃ – u₁ = 25; х₄ – u₁ = 26; х₅ – u₁ = 27; х₅ – u₂ = 26; х₆ – u₂ = 0. Полагая переменную u₂ равной нулю (u₂ = 0), получим из системы уравнений значения остальных переменных х₆ = 0; х₅ = 26; u₁ = -1; х₄ = 25; х₃ = 24; х₂ = 22; х₁ = 21.  Далее проверим выполнимость неравенств для свободных переменных:  х₁ – u₂ = 21 - 0 = 21 > 18; х₂ – u₂ = 22 – 0 = 22 > 20; х₃ – u₂ = 24 – 0 = 24 > 1; х₄ – u₂ = 25 – 0 = 25 > 24; х₆ – u₁ = 0 + 1 > 0.

Полученное решение не оптимальное, так как условие оптимальности х_j – u_i < С_ji   для свободных переменных не выполняется. Для перехода к следующему решению найдем значение коэффициентов С_ij^* = С_ji – (х_j – u_i) для свободных переменных и выявим минимальное значение. В результате получим