В работе /……/ В.Ф.Старостиным выведен безразмерный параметр ![]() ,
который для конкретного подшипника является постоянной величиной и определяет
"чистоту" качения шарика. Формула для определения этого параметра
имеет вид
,
который для конкретного подшипника является постоянной величиной и определяет
"чистоту" качения шарика. Формула для определения этого параметра
имеет вид
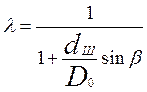
При чистом качении ![]() =1, при чистом верчении
=1, при чистом верчении ![]() = 0. В
общем случае
= 0. В
общем случае![]() будет находиться в
пределах 0<
будет находиться в
пределах 0<![]() <1. В приведенных выше
формулах не учитывается влияние на величину кинематических соотношений
центробежных сил, режима работы, смазки, износа элементов подшипника и перекоса
колец. По данным работ /1;5./ влияние этих факторов на кинематику подшипников
весьма существенно.
<1. В приведенных выше
формулах не учитывается влияние на величину кинематических соотношений
центробежных сил, режима работы, смазки, износа элементов подшипника и перекоса
колец. По данным работ /1;5./ влияние этих факторов на кинематику подшипников
весьма существенно.
Из работ /1;5/ следует, что при значительном увеличении угловой скорости вращения внутреннего кольца центробежные силы увеличивают контактные напряжения и площадки контакта на наружном кольце. Эти силы приводят также к уменьшению угла контакта с наружным кольцом и к его увеличению с внутренним.
Согласно /1/ положение оси собственного вращения шарика зависит от отношения
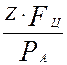
где Z - число шариков в подшипнике;
![]() - центробежная сила,
развиваемая шариком при орбитальном движении вокруг оси подшипника;
- центробежная сила,
развиваемая шариком при орбитальном движении вокруг оси подшипника;
![]() -
осевая нагрузка.
-
осевая нагрузка.
При значениях отношения 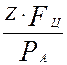 <0,1 центробежная сила
не приводит к существенному увеличению контактной площадки на наружном кольце.
Площадка контакта при этом остается меньшей, чем на внутреннем кольце. В этом
случае ось вращения шарика занимает устойчивое положение, соответствующее
чистому качению шарика по внутреннему кольцу. При значениях
<0,1 центробежная сила
не приводит к существенному увеличению контактной площадки на наружном кольце.
Площадка контакта при этом остается меньшей, чем на внутреннем кольце. В этом
случае ось вращения шарика занимает устойчивое положение, соответствующее
чистому качению шарика по внутреннему кольцу. При значениях 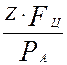 >0,1 чистое
качение происходит по наружному кольцу, так как в этом случае центробежные
силы увеличивают контактные площадки на наружном кольце.
>0,1 чистое
качение происходит по наружному кольцу, так как в этом случае центробежные
силы увеличивают контактные площадки на наружном кольце.
В работе /1/ показано, что при отношении 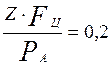 происходит
заметное изменение углов контакта. Различие углов контакта кроме
дополнительного верчения вызывает перераспределение нагрузок на желобах колец.
На рис. 2.3 показаны силы, действующие на шарик в точках контакта с внутренним
и наружным кольцами
происходит
заметное изменение углов контакта. Различие углов контакта кроме
дополнительного верчения вызывает перераспределение нагрузок на желобах колец.
На рис. 2.3 показаны силы, действующие на шарик в точках контакта с внутренним
и наружным кольцами
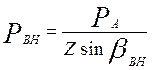 ;
;
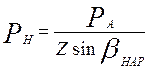 ,
,
где ![]() - углы контакта шарика с
внутренним и наружным кольцами.
- углы контакта шарика с
внутренним и наружным кольцами.
Центробежная сила ![]() , развиваемая шариком при
орбитальном движении вокруг оси подшипника, определяется по формуле /…/
, развиваемая шариком при
орбитальном движении вокруг оси подшипника, определяется по формуле /…/
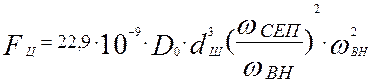
В работе /………./ для определения центробежной силы шариков приводится формула для расчета угловой скорости сепаратора с учетом углов контакта шарика с наружным и внутренним кольцом
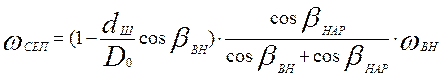
Центробежная сила связана с углами контакта следующей зависимостью
![]()
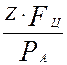
От величины углов контакта зависит величина гироскопического момента.
Согласно /……./, гироскопический момент определяется по формуле
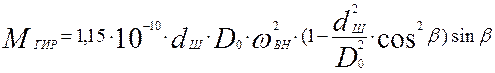
Для устранения гироскопического верчения к шарику должна быть приложена минимальная нагрузка /……./
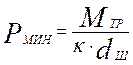
где к=0,2 - коэффициент трения при хороших условиях смазки и высокой скорости вращения.
При комбинированной нагрузке эта сила должна быть больше силы нормального давления на наименее нагруженный шарик.
Таким образом, центробежные силы в высокоскоростных радиально-упорных шарикоподшипниках вызывают осевое смещение колец, изменяют углы контакта. Действуя совместно с гироскопическим моментом, они существенно влияют на кинематику движения элементов подшипника. Различие в результатах экспериментального измерения числа оборотов сепаратора и шарика с их расчетными значениями при изменении частоты вращения, в работе /3/ объясняется проскальзыванием. В данном случае предполагается, что проскальзывание носит гидродинамический характер.
В другом случае интенсивное проскальзывание в быстроходных подшипниках при небольших осевых нагрузках объясняется гироскопической неуравновешенностью /5/.
На наш взгляд, в данном случае необходимо также учитывать изменения углов контакта под действием внешних центробежных сил.
Из расчетных зависимостей отношения скоростей вращения сепаратора и вала для радиально-упорных шарикоподшипников с сухим трением при осевой нагрузке /3/ следует, что с увеличением частоты вращения это отношение может в отдельных случаях уменьшаться и увеличиваться. Объясняется это тем, что в условиях сухого трения при осевой нагрузке могут возникать условия, при которых ведущим становится внутреннее, либо наружное кольцо.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.