Случайные процессы
1. АТС обслуживает 6000 абонентов, каждый из которых в среднем занимает линию связи в течение 1 минуты в час. Какое минимальное число каналов N надо иметь на АТС чтобы вероятность того что число поступивших в течение 1 минуты вызовов превысит число каналов было не более 0,003?
Ответ: 1) Не менее128
2. В результате проведения независимых опытов
получено 3 реализации случайной функции X(t). Получили результаты: mx(t1)=mx(t2)=15,![]() ( для всех
( для всех ![]() ), Rx(t1,t2)=Rx(τ),т.е. автокорреляционная функция зависит
только от длины интервала τ. Что можно сказать об этом процессе?
), Rx(t1,t2)=Rx(τ),т.е. автокорреляционная функция зависит
только от длины интервала τ. Что можно сказать об этом процессе?
Ответ: Это стационарный процесс в узком смысле
3. В
результате проведения трех независимых опытов получено три реализации случайных
функций ![]() . Получили результат :
. Получили результат :
![]() ,
, ![]() (для всех
(для всех ![]() ),
), ![]() , т.е.
автокореляционная функция зависит только от длинны интервала
, т.е.
автокореляционная функция зависит только от длинны интервала ![]() . Что можно сказать об
этом процессе?
. Что можно сказать об
этом процессе?
Ответ: 3) Это стационарный процесс в узком смысле.
4. Время корреляции определяют как:
Ответ: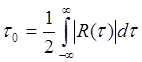
5. Генератор тока рассчитан на постоянную
мощность 200 единиц. Действительное потребление тока характеризуется мощностью W(t),
которая является нормальной случайной функцией времени. В том случае, когда
потребляемая мощность превосходит расчетную, включается резервный генератор,
мощность которого практически не ограниченна. Определить среднюю энергию
затрачиваемую генератором в течении одного выброса функции W(t) за
уровень 200 единиц, если математическое ожидание ![]() Вт, а корреляционная
функция
Вт, а корреляционная
функция ![]()
Ответ: 32,5
6. Дана случайная комплексная функция Z(t)=X(t)+iY(t). Как определяется математическое ожидание и дисперсия этой функции в общем виде.
Ответ: ![]()
7. Два случайных процесса соответственно
характеризуются следующими корреляционными функциями: ![]() . Какой случайный
процесс является дифференцируемым?
. Какой случайный
процесс является дифференцируемым?
Ответ: Y(t)
8.
Если стационарная случайная функция ![]() обладает эргодическим
свойством, то ее мат. ожидание равно:
обладает эргодическим
свойством, то ее мат. ожидание равно:
Ответ: 4) 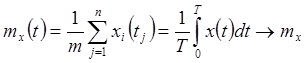 при
при ![]()
9. Если стационарная случайная функция X(t) обладает эргодическим свойством, то значение корреляционной функции R(τ) при любом τ приближенно равно:
Ответ: 2) 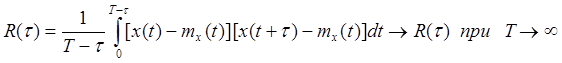
10. Заданы
случайные функции![]() -
некоррелированные стандартизированные случайные величины. Найти нормированную
взаимную корреляционную функцию
-
некоррелированные стандартизированные случайные величины. Найти нормированную
взаимную корреляционную функцию ![]()
Ответ: 4) ![]()
11. Имеется два случайных процесса с корреляционной функцией Rxy(t1,t2)=cos2(ω1t1+ω2t2). Найти корреляционную функцию Ryx(t1,t2).
Ответ: 1) Ryх(t1,t2)=cos2(w1t1 +w2t2)
12. Как изменятся основные характеристики случайного процесса в общем случае, если его значения умножить на 5:
Ответ: Мат,ожид. умножится на 5,дисперсия ув. в 5
раз, среднекв. отклон. умножится на ![]()
13. Как изменятся основные характеристики случайного процесса в общем случае, если его значение умножить на 2.
Ответ: 4)
Мат.ожид. умножится на 2, дисперсия увел. в 4 раза, среднеквадр.отклон. умн. на
![]()
14. Как изменяется среднеквадратическое отклонение случайного процесса, если его значение умножить на -5?
Ответ: 3) Умножится на 5
15. Каково воздействие на систему описывается функцией вида 1(t,t1):
16. Какая величина не является вероятностной характеристикой выбросов случайных процессов?
Ответ: Среднее знач. проц. в наблюдаемый период
17. Какая случайная функция называется полностью определенной:
Ответ: Если заданы все К-мерные законы распределения(К=1,2,…)
18. Какое воздействие на систему описывается функцией вида
![]()
Ответ: Единичное ступенчатое воздействие
19. Какое воздействие на систему описывается так называемый дельта- функции:
20. Какое из ниже приведенных выражений для спектральной плоскости верно:
Ответ: 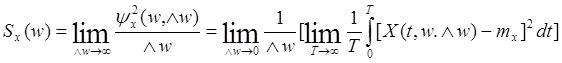
21. Какое преобразование не относится к линейно-однородным операторам.
Ответ: 3) Y(t)=X(t)+![]()
22. Какое утверждений соответствует правилу составления уравнения Колмогорова?
Ответ: 3) Производная вероятности любого состояния равна сумме потоков вероятностей переводящих систему в это состояние минус сумму всех потоков веротностей, выводщих систему из этого состояния.
23. Какой из нижеперечисленных процессов является недетерминированным?
Ответ: Изменение высоты волн на поверхности моря
24. Корреляционная функция ![]() :
:
Ответ:
25. Корреляционная функция комплексной случайной функции Z(t)=X(t)+iY(t) определяется как
Ответ: 2) Rz(t1,t2)=Rx(t1,t2)+Ry(t1,t2)+i[Rxy(t2,t1)-Rxy(t1,t2)]
26. Марковская цепь называется однородной, если:
Ответ: переходные вероятности не зависят от номера шага
27. Может ли при каких - либо значениях аргумента быть:
1. корреляционная функция отрицательной?
2. спектральная плотность отрицательной?
3. нормированная корреляционная функция отрицательной?
Ответ: 1) Да,нет,да
28. Может ли при каких — либо значениях аргумента быть:
1. плотность распределения отрицательной?
2. дисперсия больше единицы?
3. среднее квадратическое отклонение меньше нуля?
Ответ: 3) Нет,да,нет
29. Может ли при каких либо значениях аргумента быть:
1. Плотность распределения отрицательной?
2. Дисперсия больше единицы?
3. Среднее квадратическое отклонение меньше нуля ?
Ответ: 3) Нет,да,нет
30. На
вход линейной динамической системы, описываемой
уравнением ![]() поступает
стационарный случайный процесс с корреляционной функций
поступает
стационарный случайный процесс с корреляционной функций ![]() и математическим ожиданием mх = 5. Найти my , Dy выхода
системы.
и математическим ожиданием mх = 5. Найти my , Dy выхода
системы.
31. На вход
линейной динамической системы, описываемой уравнением
![]() поступает стационарный сигнал с автокорреляционной
функцией
поступает стационарный сигнал с автокорреляционной
функцией ![]() . Найти спектральную плотность, характеризующую стационарный сигнал на
выходе системы.
. Найти спектральную плотность, характеризующую стационарный сигнал на
выходе системы.
Ответ: 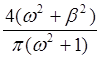
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.