Оптимизация систем массового обслуживания. Приобретение навыков расчета и оптимизации характеристик реальных систем массового обслуживания

Министерство высшего и профессионального образования РФ

Тульский государственный университет

Кафедра прикладной математики и информатики

СЛУЧАЙНЫЕ  ПРОЦЕССЫ

Лабораторная работа №5

Выполнил ст. гр.                                                            

Проверил к.т.н., доц.                                                                               А

Тула 2001

ОПТИМИЗАЦИЯ   СИСТЕМ   МАССОВОГО   ОБСЛУЖИВАНИЯ

I. ЦЕЛЬ  РАБОТЫ.

Приобретение навыков расчета и оптимизации характеристик реальных систем массового обслуживания.

II. ЗАДАНИЕ.

На основе результатов исследования потока заявок в реальной системе массового обслуживания и построения математической модели, полученных в работе №4, оптимизировать данную систему: парикмахерскую.

Необходимо:

1.  По вычисленным основным параметрам входных и выходных потоков построить математическую модель системы и определить вероятности ее состояний. Рассчитать основные показатели эффективности функционирования СМО, включая экономические оценки;

2.  Предложить 1-3 варианта усовершенствования системы, с целью повышения ее эффективности функционирования по экономическим параметрам (критериям). Произвести экономическую оценку различных вариантов организации работы системы и выбрать наилучший из них.;

3.  Проанализировать полученные результаты.

III. РЕШЕНИЕ.

На основании работы №4 имеем следующие данные.

В парикмахерскую приходят клиенты с интенсивностью клиента за 30 минут. В салоне работают мастера. Помещение парикмахерской может разместить только 10 человек, ожидающих своей очереди, и приходящие клиенты не могу ждать в очереди более 1 часа. Среднее время одной стрижки составляет 21.9 минут. Для улучшения обслуживания были сделаны два предположения:

1)  нанять еще одного мастера;

2)  нанять еще двух мастеров.

Найм одного мастера обойдется в 20 тыс.руб. в год. Потери от отказа в своевременном обслуживании одного клиента 80 руб. Потери от простоя одного мастера 7 руб в час. Из трех возможных вариантов системы (три, четыре или пять мастеров) необходимо выбрать лучший по критерию минимальных приведенных затрат. ()

Все величины приведем к годовому периоду времени. Имеем:

-   клиентов в час, за рабочий день (10 ч.): 70 кл., за год: 24920;

-  среднее обслуживания одного клиента: 21,9мин или 0,365ч., тогда .

Имеем СМО смешанного типа с ограничениями по длине очереди (человек) и времени ожидания в очереди (час). Ее характеристики:

;  ;  ;  ;  ;  .

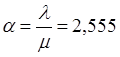Коэффициент загрузки системы: .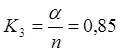

1.  Определим вероятности отказов в рассматриваемых случаях:

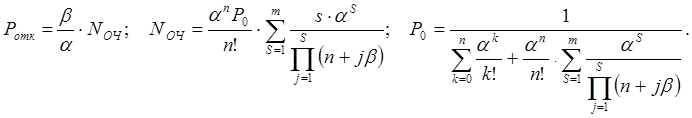
a)    

b)    

c)    

2.  Определим простои системы:

a)    

простои за год составляют: ч.

b)     Здесь простои мастеров будут складываться следующим образом: ; 

c)     простои за год  в этом случае ; 

Конечные результаты расчетов сведем в следующую таблицу:

Выгоднее иметь пять мастеров, т.е. необходимо нанять еще двух.