Анализ результатов с физической интерпретацией выводов. Приобретение навыков вычисления некоторых вероятностных характеристик случайных процессов

Министерство общего и профессионального образования

Российской Федерации

Тульский государственный университет

КАФЕДРА ПРИКЛАДНОЙ МАТЕМАТИКИ И ИНФОРМАТИКИ

СЛУЧАЙНЫЕ ПРОЦЕССЫ

ЛАБОРАТОРНО-ПРАКТИЧЕСКИЕ РАБОТЫ

МЕТОДИЧЕСКИЕ УКАЗАНИЯ

для студентов всех форм обучения

специальностей

"Прикладная математика и информатика",

"Математические методы и исследование операций в экономике"

Тула 1999

ВВЕДЕНИЕ

Во многих отраслях практической деятельности часто имеют дело с явлениями, на которые оказывают влияние множество факторов, не поддающихся строгому учету и контролю. Объективное суждение о закономерностях таких процессов или систем возможно лишь на основе вероятностно-статистического анализа исследуемого явления. Современный специалист должен хорошо ориентироваться в вопросах количественного описания вероятностных процессов, уметь видеть закономерности в случайных явлениях, владеть навыками обработки статистических данных.

Предлагаемые задания лабораторных работ по курсу "Случайные процессы" - дают возможность практического закрепления и расширения знаний использования математических методов теории случайных процессов для решения практических задач в некоторых областях деятельности.

Каждый студент индивидуально, согласно порядковому номеру в журнале группы, выполняет соответствующий вариант задания. Допустимо использовать (по согласованию с преподавателем) вместо предложенных другие статистические данные, отражающие реальный физический (экономический, технический и др.) процесс.

После выполнения каждой работы студентом оформляется отчет, который должен содержать:

- цель и задачи работы;

- физическую постановку и имеющиеся исходные данные;

- алгоритм решения задачи;

- наглядное (табличное, графическое и др.) представление полученных результатов;

- анализ результатов с физической интерпретацией выводов.

Отчет оформляется в соответствии с общими требованиями к студенческим работам.

При защите работ студент должен знать соответствующие теоретические положения, хорошо ориентироваться в физическом смысле полученных результатов, отвечать на вопросы.

РАБОТА № 1. ВЫЧИСЛЕНИЕ ВЕРОЯТНОСТНЫХ

ХАРАКТЕРИСТИК СЛУЧАЙНЫХ ПРОЦЕССОВ

I. ЦЕЛЬ РАБОТЫ

Приобретение навыков вычисления некоторых вероятностных характеристик случайных процессов.

II. ЗАДАНИЕ НА РАБОТУ

Задача. Мощность угольного пласта с математическим ожиданием (средним значением)  [м] является нормальной стационарной случайной функцией по направлению отработки с автокорреляционной функцией (АКФ)  (t- в метрах). Скорость продвижения забоя равна V [м/ч]. В текущий момент обработки пласта его мощность равна  [м].

Определить вероятность того, что через t часов работы мощность пласта будет больше  [м].

III. ВАРИАНТЫ ЗАДАНИЯ

Варианты заданий приведены в табл.1.1.

Таблица 1.1

Варианты исходных данных задачи

№ n/n	Значения параметров задачи
	, м	a, м2	b, м2	c, м-1	V, м/ч	, м	t, ч	, м
1	4.5	1.9	0.14	0.2	1.5	3.6	1.2	3.8
2	4.3	1.7	0.13	0.8	1.3	3.4	1.7	3.6
3	4.2	1.8	0.44	0.2	0.9	3.8	1.5	4.3
4	5.4	2.1	0.35	0.4	1.2	3.5	1.7	5.2
5	5.1	1.7	0.5	0.1	1.5	3.6	1.2	3.8
6	4.1	1.8	0.45	0.2	1.4	3.4	0.7	3.6
7	4.7	2.3	0.2	0.7	2.3	3.8	1.5	4.2
8	3.8	1.7	0.3	0.5	0.8	3.6	1.2	3.9
9	6.5	2.4	0.1	0.2	0.7	5.6	1.2	5.8
10	6.3	1.7	0.4	0.1	1.3	5.4	1.4	5.6
11	6.2	1.8	0.5	0.2	0.2	5.8	1.5	5.3
12	6.4	2.1	0.17	0.2	2.3	6.5	0.4	6.2
13	6.1	1.6	0.2	0.1	1.5	6.9	1.2	6.8
14	4.5	1.4	0.1	0.2	1.5	3.6	1.2	3.8
15	4.3	1.7	0.3	0.1	1.3	3.4	1.7	3.6
16	4.2	1.8	0.35	0.2	2	3.8	0.5	4.3
17	5.4	2	0.27	0.2	3	5.5	0.7	5.2
18	5.1	1.7	0.28	0.1	1.5	3.6	1.2	3.8
19	4.2	1.8	0.5	0.2	0.8	3.8	1.5	4.3
20	5.4	2.1	0.12	0.22	1.2	3.5	0.7	5.2
21	5.1	1.7	0.18	0.1	1.5	3.6	1.2	3.8
22	4.1	1.8	0.25	0.2	1.4	3.4	1.8	3.6
23	4.7	2.3	0.36	0.2	2.3	3.8	0.6	4.2
24	7.4	2.1	0.35	0.22	1.2	7.5	1.7	7.2
25	7.1	1.7	0.18	0.1	1.5	7.6	1.2	6.8

IV. МЕТОДИЧЕСКИЕ УКАЗАНИЯ

Рассмотрим методику решения аналогичной задачи для конкретных данных. Пусть  = 3,4 м; V = 1,5 м/ч. В текущий момент обработки пласта его мощность равна 4 м. Определим вероятность того, что через 2 часа работы мощность пласта будет больше 4,4 м, если a = 2м²; b= 0,1м²; с =0,2м^-1.

Решение. Обозначим x₁ = X(t₀) = 4м; x₂ = X(t₀ + 2).

Для условного закона распределения x₂ имеем 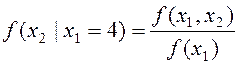, где f(x₁,x₂) - нормальный закон распределения системы случайных величин с корреляционной матрицей 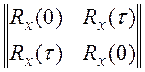, где t = 2часа×1,5м/час = 3м.

Искомая вероятность определится соотношением: .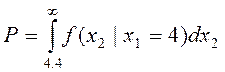

Условный закон распределения определим по выражению:

.

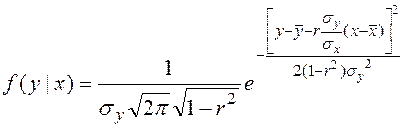Вычислим неизвестные параметры этой формулы, используя соответствующие вероятностно-статистические таблицы.

Имеем .

Тогда .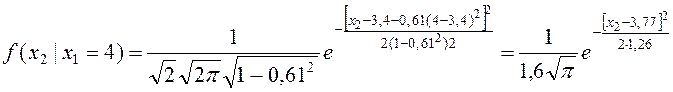

Используя таблицу функции Лапласа, определяем искомую вероятность

.

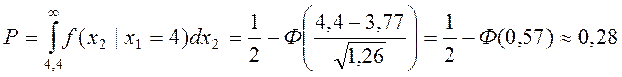РАБОТА № 2. ПРОХОЖДЕНИЕ СЛУЧАЙНЫХ ПРОЦЕССОВ

ЧЕРЕЗ ЛИНЕЙНЫЕ ДИНАМИЧЕСКИЕ СИСТЕМЫ

I. ЦЕЛЬ РАБОТЫ

Приобретение навыков расчета выходных характеристик случайных процессов по известным входным характеристикам и заданной модели динамического объекта.

II. ЗАДАНИЕ НА РАБОТУ

Объект описан дифференциальным уравнением:

.

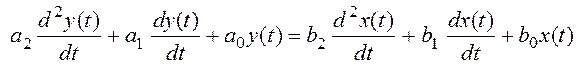На вход объекта подается случайное напряжение с математическим ожиданием m_x и корреляционной функцией

Определить математическое ожидание, корреляционную функцию, спектральную плотность, среднее квадратическое отклонение и дисперсию напряжения на выходе объекта.

III. ВАРИАНТЫ ЗАДАНИЯ

Варианты заданий приведены в табл.2.1.

Таблица 2.1

Варианты значений параметров задачи

№	a0	a1	a2	b0	b1	b2	mx		a
1	-4	2	3	5	6	12	15	6	12
2	3	7	8	-3	-1	7	23	4	7
3	13	23	5	2	8	15	42	8	15
4	7	8	1	3	5	2	223	5	2
5	34	18	15	9	36	1	127	36	1
6	8	1	-3	2	7	0	62	7	2
7	6	5	8	-3	-1	3	15	4	3
8	44	5	8	6	8	1	23	8	1
9	1	-3	-1	-4	2	3	42	2	3
10	2	2	8	3	7	8	223	7	8
11	-3	53	5	-7	-9	2	127	9	2
12	2	8	-4	3	1	0	62	10	2
13	3	5	3	8	1	0	88	15	3
14	-4	2	3	5	2	3	35	2	3
15	3	7	8	2	7	8	42	7	8
16	-7	-9	2	7	-9	2	67	12	2
17	3	1	2	-9	8	15	49	8	15
18	5	-4	2	1	5	2	15	5	2
19	2	3	7	1	-4	0	41	4	2
20	7	-27	-9	0	10	8	30	10	8
21	29	3	1	8	20	5	8	2	5
22	2	3	1	3	31	-4	53	3	6
23	7	8	1	8	1	8	18	4	8
24	3	7	8	-4	7	45	74	7	5
25	-9	2	0	2	0	1	32	5	1

IV. МЕТОДИЧЕСКИЕ УКАЗАНИЯ

Общей формой описания элементов динамических систем является дифференциальное уравнение, связывающее входной и выходной процесс

.             (2.1)

Пусть вход и выход линейной динамической системы связаны соотношением (2.1) или в операторной форме: 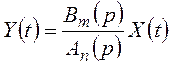, где  и  - многочлены степени m и n соответственно от 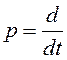, т.е. от оператора дифференцирования.

Тогда частотная характеристика системы определяется следующим образом:  .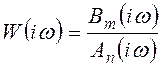

Если на вход системы поступает функция X(t) с математическим ожиданием  и корреляционной функцией , то  и  на выходе системы определяются по следующему алгоритму:

1. ;

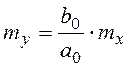2. ;

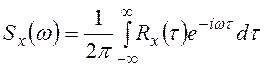3. ;

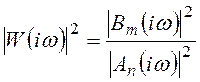4. ;

5. ;

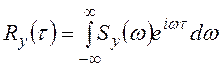6.  .

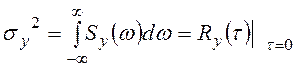Так как вычисление интегралов в указанных выше формулах может представлять в некоторых случаях технические трудности, то целесообразно использовать для вычисления интегралов вычеты.

Напомним условия применения вычетов к вычислению интегралов (residue - вычет ).

Пусть а - полюс n - го порядка функции . Вычет функции  относительно ее полюса n - го порядка вычисляется