Тульский государственный университет
Кафедра прикладной математики и информатики
Выполнил ст. гр.
Проверил к.т.н., доц. А
Тула 2001
РЕШЕНИЕ ЗАДАЧ О ВЫБРОСАХ
I. ЦЕЛЬ РАБОТЫ.
Приобретение навыков расчета характеристик случайного процесса при выходе его за определенные границы.
II. ЗАДАНИЕ.
Содержание железа в рудном блоке длинной ![]() по направлению его отработки является
нормальной случайной функцией со средним значением
по направлению его отработки является
нормальной случайной функцией со средним значением ![]() и
автокорреляционной функцией
и
автокорреляционной функцией
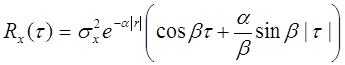 (τ – в метрах).
(τ – в метрах).
Руда считается кондиционной, если содержание железа в
ней не ниже ![]() .
.
Определить:
1.
Сколько раз в среднем за
время отработки блока содержание железа будет выходить за пределы ![]() %;
%;
2.
Вероятности Р0,
Р1, Р2 того, что на первых К метрах не будет
ни одного выхода содержания железа за пределы ![]() %;
будет один выход; два выхода.
%;
будет один выход; два выхода.
3. Среднюю продолжительность поступления некондиционной руды;
4.
Сколько раз в среднем за
время отработки блока содержание железа будет равно ![]() .
.
Здесь
![]()
III. РЕШЕНИЕ.
1.Искомое число выбросов ![]() ,
где коэффициент 2 появляется в следствии того, что надо учитывать как
выбросы снизу вверх за уровень
,
где коэффициент 2 появляется в следствии того, что надо учитывать как
выбросы снизу вверх за уровень ![]() , так и выбросы
сверху вниз за уровень
, так и выбросы
сверху вниз за уровень ![]() .
.![]() –
длина блока.
–
длина блока. ![]() – среднее число выбросов
стационарного нормального процесса в единицу времени, определяемое следующим
образом:
– среднее число выбросов
стационарного нормального процесса в единицу времени, определяемое следующим
образом:
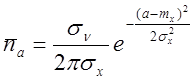 , где
, где 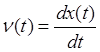 .
.
Подставляя данные задачи в формулу, имеем:
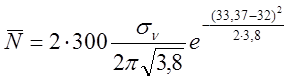 .
.
Определим ![]() :
:
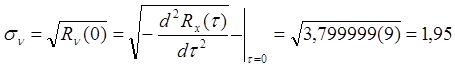 .
.
Тогда число выбросов:
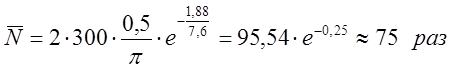 .
.
2.
Считая допустимым приближенно пользоваться законом
Пуассона, получаем среднее число выбросов на первых ![]() :
:
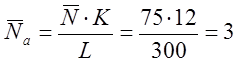
вероятность того,
что на первых ![]() не будет ни одного выброса
за пределы
не будет ни одного выброса
за пределы ![]() :
:
![]()
вероятность того,
что на первых ![]() будет один выброс:
будет один выброс:
![]()
вероятность того,
что на первых ![]() будет два выброса:
будет два выброса:
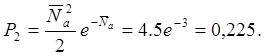
Некоторой проверкой допустимости
применения закона Пуассона в данном случае может служить тот факт, что для
среднего расстояния между выбросами 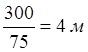 нормированная
корреляционная функция при
нормированная
корреляционная функция при ![]() равна нулю:
равна нулю: ![]()
3. Средняя длительность выброса нормального случайного процесса Х(t) за уровень а определяется формулой:
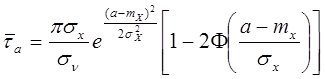 .
.
В данном случае ![]() ;
; 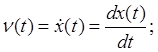
![]()
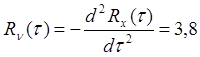
Тогда средняя продолжительность поступления некондиционной руды составляет:
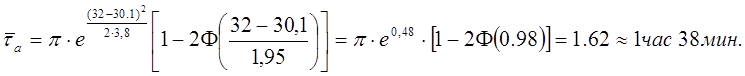
4. Искомое число равно числу выбросов в обе стороны за нулевой уровень.
![]() ;
; 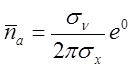 ;
; 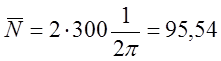 .
.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.