Случайные процессы. Время корреляции. Математическое ожидание и дисперсия функции в общем виде, страница 2

32. На вход цепи аппаратов обогатительной фабрики непрерывно подаётся руда со средним содержанием железа 27%. Содержание железа в руде является нормальной случайной функцией времени с автокорреляционной функцией  - в часах. Руда считается кондиционной,  если  содержание железа  >=25%. Определить продолжительность поступления некондиционной руды.

     Ответ: 4) 26 мин.

33. Найти корреляционную функцию случайного стационарного процесса Х(t), если его спектральная плотность , постоянна на интервале (0,1) и равна 1, а вне этого интервала0.      Ответ: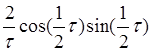

34. Найти переходную функцию h(t) элемента, описываемого уравнением

     Ответ: 1) h(t)=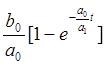

35. Найти характеристики элементарной случайной функции Y(t)=Vcos+Usin, где U, V -некоррелированные случайные величины с характеристиками: - неслучайная величина. Найти .

     Ответ: R_y(t,t¹)=

36. Напряжение на выходе устройства является случайным процессом с m_x(t)=0, R_x(τ)=5∙e^-0.1|x| cos(2τ), τ - в секундах. Определить, сколько раз в среднем в течении времени Т=8 мин. Напряжение на выходе будет равно нулю.

     Ответ: 4) 680раз

37. Напряжение является нормальным стационарным процессом с нулевым математическим ожиданием и корреляционной функцией: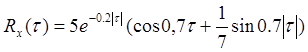.   Сколько раз  в  среднем за  8  минут напряжение будет принимать нулевое значение?

     Ответ: 3) 108.

38. Нормальный      стационарный      случайный      процесс      Х(t)       имеет характеристики 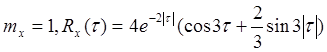  Вычислить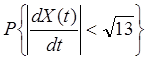

     Ответ: 3) 0,383

39. Общей   формой   описания   элементов  динамических   систем является дифференциальное    уравнение,    связывающее   входной   и   выходной  процесс, укажите верный вариант его записи:

     Ответ:

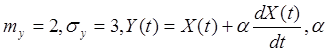40. Определить, являются ли стационарными случайные функции случайная величина с характеристиками -не случайная величина.

     Ответ: X(t),Y(t)-не стационар.

41. По      заданной      спектральной      плотности      случайного     процесса

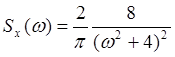
найти его дисперсию.

     Ответ: 1) 0,5

42. Пусть имеются три конкурирующих изделия Х1,Х2;.Х3- С целью определения спроса на эти  изделия произведён опрос 100 человек. Оказалось, что изделие X1 покупает 50 человек, изделие X; —20 человек, а Хз — 30 человек. Предположим, что поведение покупателей в каждый следующий месяц обусловлено только их поведением в предыдущий месяц. По истечении месяца оказалось, что из 50 человек, покупавших изделие Х1, 45 продолжают его покупать, 4 человека, стали покупать изделие X2 и 1 - изделие Х3 . Из 20 человек, покупавших изделие Х2 6 человек продолжают его покупать, 8 стали покупать изделие Х1 ,6 -изделие Хз. Из 30 человек. покупавших изделие Хз, б человек продолжают его покупать, 21 человек стал покупать изделие Х1 , 3 -изделие X2; . Требуется найти вероятности потребности в изделиях по истечении месяца.

     Ответ: 2) P₁=0,82;P₂=0,11;P₃=0,07

43. Работа линейной динамической системы описывается дифференциальным уравнением:  . На вход системы  подается случайное напряжение с математическим ожиданием m_x=220 и корреляционной функцииR_x(τ)=16e^-3|x|. Определить математическое ожидание и дисперсию напряжения на выходе системы