Ответ: my=220,Dy=4
44. Рассматривается неслучайная, величина а, как частный случая с. п.:
Х(t) = а; найти ее характеристика, а именно М[Х(t)],D(t).
Ответ: 1) a,0
45. Связь входного и выходного сигналов описывается уравнением:
Ответ: ![]()
46.Случайная
функция Х(t) имеет
характеристики ![]() = 1 и
= 1 и![]() . Определить
характеристики случайной функции:
. Определить
характеристики случайной функции:
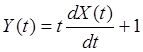 ,а именно
,а именно ![]()
Ответ: my=1;Ry(t,t1)=a2tt1ea(t+t1)
47. Система
представляет собой техническое устройство Т, которое может находиться в
одном из двух состояний: S1 - Т -
исправно, S2 - Т -неисправно.
На систему действуют два пуассоновских независимых потока: поток отказов
с интенсивностью ![]() и поток
восстановлений с интенсивностью
и поток
восстановлений с интенсивностью ![]() .
Найти вероятность того, что устройство будет неисправно, если
.
Найти вероятность того, что устройство будет неисправно, если ![]() и P1(0)=1.
и P1(0)=1.
Ответ: 4) P1(t)=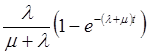
48. Случайный процесс X(t) = Vt + a , где V –
случайная величина с характеристиками mr=10 и ![]() . Найти характеристики
Y(t)=
. Найти характеристики
Y(t)=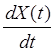 .
.
Ответ: Ry=1,Dy=1,my=1+t
49. Случайный
процесс имеет автокорреляционную функцию ![]() .Какова автокорреляционная функция
.Какова автокорреляционная функция ![]()
![]()
Ответ: 2) ![]()
50. Случайная
функция имеет вид ![]() , где X - случайная величина,
распределённая по нормальному закону,
, где X - случайная величина,
распределённая по нормальному закону, ![]() Каково
математическое ожидание случайной функции Y(t)?
Каково
математическое ожидание случайной функции Y(t)?
Ответ: 1) ![]()
51. Случайная
функция X(t) имеет
характеристики ![]() .
Определить характеристика случайной функции:
.
Определить характеристика случайной функции: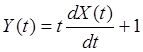 .
. ![]()
Ответ: my=1,Ry(t,t1)=4tt1e2(t+t1)
52. Случайная функция X(t) имеет
характеристики: mx(t)=0, Rx(t, t’)=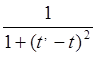 .
Определить, стационарны ли случайные функции X(t) и
.
Определить, стационарны ли случайные функции X(t) и 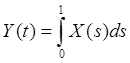
53. Случайная функция X(t) с
математическим ожиданием mx(t)=t2-1 подвергается преобразованию 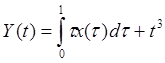 . Определить
. Определить ![]() .
.
Ответ: 1) my(t)=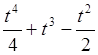
54. Случайная
функция X(t) задана
выражением ![]() , где V — случайная
величина с характеристиками
, где V — случайная
величина с характеристиками ![]() Найти
Найти
![]() случайного процесса Y(t)=X(t)+3
случайного процесса Y(t)=X(t)+3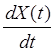
Ответ: 4) my(t)=2coswt-6wsinwt,Dy(t)=9(coswt-3wsinwt)2
55. Спектральная плотность изменения температуры
воздуха в летний период (температура фиксировалась ежедневно в 12:00 часов)
выражается зависимостью: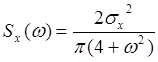 .
Определить корреляционную функцию этого процесса.
.
Определить корреляционную функцию этого процесса.
Ответ: 3)![]()
56. Среднее значение случайного процесса в момент времени t1 может быть найдено:
Ответ: mx(t1)=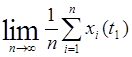
57. Укажите верное выражение для спектральной плотности дисперсии:
Ответ: 1) 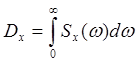
58. Укажите
правильную зависимость для функции ![]()
![]() если взаимная
спектральная плотность равна:
если взаимная
спектральная плотность равна: 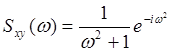
Ответ: 1)
59. Укажите правильное определение взаимной спектральной плотности.
Ответ: Sxy(![]() )=
)=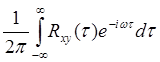
60.Функция комплексной переменной, определяемая как отношение преобразованных по Лапласу выходного сигнала к входному сигналу при нулевых начальных условиях, называется .
Ответ: 4) передаточной функцией
61. Элементарная случайная функция У(т) имеет
вид ![]() ,t>0,
где X - случайная
величина, распределенная по показательному закону с
плотностью:.
,t>0,
где X - случайная
величина, распределенная по показательному закону с
плотностью:.![]() Найти
характеристику
Найти
характеристику ![]()
Ответ: ![]() =
=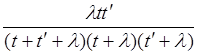
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.