Моделирование задачи дифракции упругих волн на жестком цилиндре в упругой среде. Приобретение практических навыков моделирования волновых процессов и их обработки с помощью ЭВМ

Федеральное агентство по образованию

Государственное образовательное учреждение

высшего профессионального образования

Тульский государственный университет

Кафедра прикладной математики и информатики

Математическое моделирование

Лабораторная работа №3

МОДЕЛИРОВАНИЕ ЗАДАЧИ ДИФРАКЦИИ

УПРУГИХ ВОЛН НА ЖЕСТКОМ ЦИЛИНДРЕ

В УПРУГОЙ СРЕДЕ

Вариант 13

Выполнил студент группы :                                        

Проверил:                                                                                        

Тула 2005

ЦЕЛЬ РАБОТЫ

Приобретение практических навыков моделирования волновых процессов и их обработки с помощью ЭВМ.

ТЕОРЕТИЧЕСКАЯ СПРАВКА

Рассмотрим задачу рассеяния плоской гармонической волны сжатия, потенциал которой определяется выражением

,                                                  (1)

где 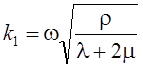– волновое число, w – круговая частота, на жесткое круговое  цилиндрическое включение, впаянное безграничную упругую среду с плотностью r и константами Ламе l и m. Встречаясь с поверхностью препятствия, подающая нормально к оси цилиндра волна порождает отраженные волны сжатия и сдвига. Полное волновое поле создает напряженно-деформированное состояние в упругой среде в окрестности включения.

Рассмотрим волновое уравнение

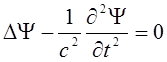.                                               (2)

Представим функцию Y =  в виде  y = . Подставляя эту запись в уравнение (2), получим

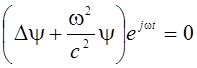
или

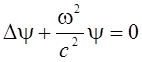.                                                        (3)

Полученное уравнение называется уравнением Гельмгольца. В полярных координатах уравнение (3) имеет вид

.

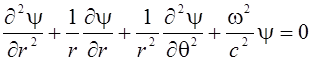Для нахождения решения этого уравнения воспользуемся методом разделения переменных:  , k² = .                                

.                                

;

                                      

.

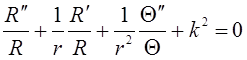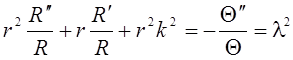
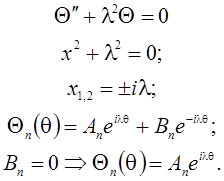
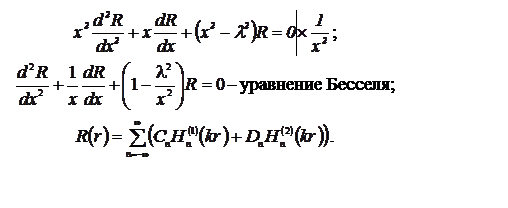
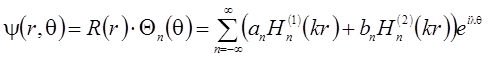В зависимость от конкретной задачи, можно выбрать наиболее подходящие функции, являющиеся решением уравнения Бесселя.

Рассмотрим систему уравнений Гельмгольца для падающей и отраженной волн

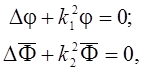                                                    (4)

при граничных условиях

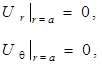                                                       (5)

где  – нормальная и касательная компоненты вектора смещения упругой среды, r, q, z – цилиндрические координаты.

Так как упругое тело находится в условиях плоской деформации, в плоскости хОу, то , где U – вектор смещения,  – единичный вектор оси z. В этом случае векторный потенциал , где – скалярная функция,. Тогда вместо (2) получим систему двух скалярных уравнений

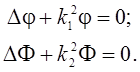                                                    (6)

Если решение (4) известно, то смещения и напряжения определяются по формулам

.

;     .

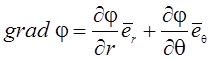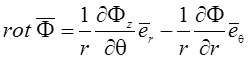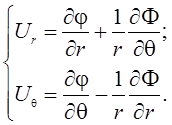                                                 (7)

;

.

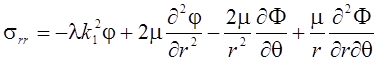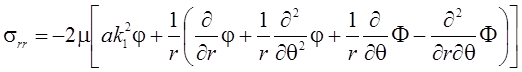
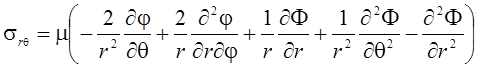Общее решение уравнений (6) с учетом условий излучения возьмем в форме рядов

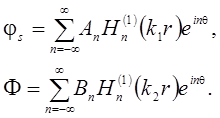                                             (8)

где – неизвестные постоянные, определяемые из граничных условий. Множитель  здесь и ниже опущен.

Граничные условия (5) на основании (7) запишутся в виде

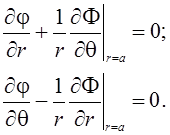                                                 (9)

Падающую волну представим в виде ряда Фурье

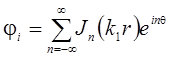.                                             (10)

Удовлетворяя условиям (9), получаем алгебраическую систему уравнений для определения :

,                                                (11)

где

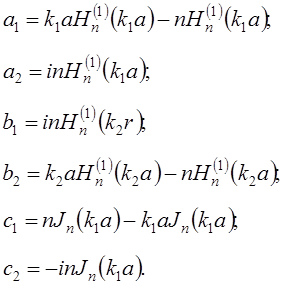
Решив систему (11), найдем неизвестные постоянные , и, следовательно, потенциалы . Тем самым поставленная задача будет решена.  

ПРОГРАММНЫЙ МОДУЛЬ НА ЯЗЫКЕ MAPLE И РЕЗУЛЬТАТЫ

РАБОТЫ ПРОГРАММЫ

> restart;

> H1:=(x,y)->HankelH1(x,y):

J:=(x,y)->BesselJ(x,y):

> A:=(q,x,y,t)->q*H1(x,y)*exp(I*x*t):

B:=(x,y,t)->J(x,y)*exp(I*x*t):

C:=(q,x,y,t)->(q*H1(x,y)+J(x,y))*exp(I*x*t):

> DifA_T:=(q,x,y,t)->I*q*H1(x,y)*x*exp(I*x*t):

DifA_r_T:=(q,x,y,t)->I*q*(-H1(x+1,y)+x*H1(x,y)/y)*x*exp(I*x*t):

> DifB_r:=(x,y,t)->(-J(x+1,y)+x*J(x,y)/y)*exp(I*x*t):

DifB_T2:=(x,y,t)->-J(x,y)*x^2*exp(I*x*t):

> DifC_r:=(q,x,y,t)->(q*(-H1(x+1,y)+x*H1(x,y)/y)

                        -J(x+1,y)+x*J(x,y)/y)*exp(I*x*t):

DifC_T2:=(q,x,y,t)->-(q*H1(x,y)+J(x,y))*x^2*exp(I*x*t):

> lambda1:=11.1*10^11:

mu1:=8.1*10^11:

rho1:=7.7:

> V1:=proc(f,omega,r,a,theta,rho,lambda,mu)

local n,k1,k2,c,b,d,SigmaRR,SigmaRRo,BSigmaRR,BSigmaRRo,U;

d:=array(1..2):

k1:=omega*sqrt(rho/(lambda+2*mu)):

k2:=omega*sqrt(rho/mu):

SigmaRRo:=0;

BSigmaRRo:=0;

for n from -f to f do

b:=matrix(2,2,[k1*a*H1(n,k1*a)-n*H1(n,k1*a),I*n*H1(n,k2*a),

                I*n*H1(n,k1*a),k2*a*H1(n,k2*a)-n*H1(n,k2*a)]):

c:=vector(2,[n*J(n,k1*a)-k1*a*H1(n,k1*a),-I*n*J(n,k1*a)]):

d:=evalm(c&*(b^(-1))):

SigmaRR:=SigmaRRo-2*mu*

  (a*k1^2*C(d[1],n,k1*r,theta)+1/r*

  (DifC_r(d[1],n,k1*r,theta)+1/r*DifC_T2(d[1],n,k1*r,theta)

  +1/r*DifA_T(d[2],n,k2*r,theta)-DifA_r_T(d[2],n,k2*r,theta))):

BSigmaRR:=BSigmaRRo-2*mu*(a*k1^2*B(n,k1*a,theta)+1/a*

  (DifB_r(n,k1*a,theta)+1/a*DifB_T2(n,k1*a,theta))):

SigmaRRo:=SigmaRR;

BSigmaRRo:=SigmaRR;

end do;

U:=evalf(abs(SigmaRR/BSigmaRR));

end proc:

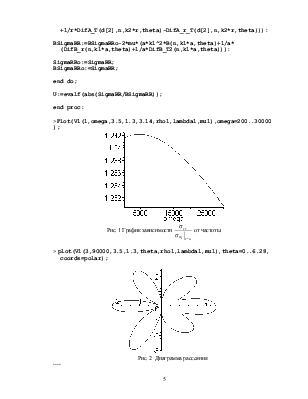
>Plot(V1(1,omega,3.5,1.3,3.14,rho1,lambda1,mu1),omega=200..30000);

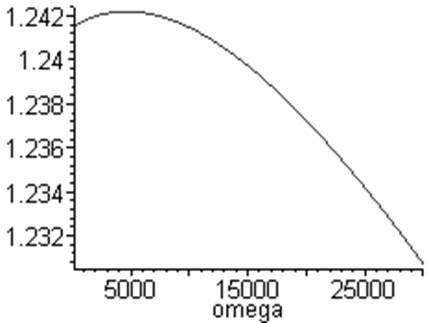
Рис. 1 График зависимости 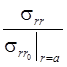 от частоты.

> plot(V1(3,90000,3.5,1.3,theta,rho1,lambda1,mu1),theta=0..6.28,

  coords=polar);

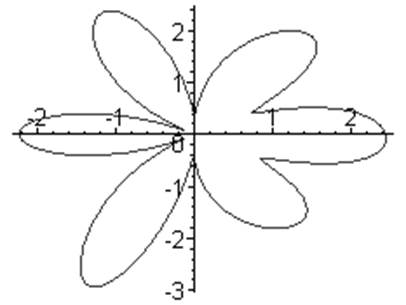
            Рис. 2  Диаграмма рассеяния

----