Моделирование задачи нахождения стационарного температурного поля неограниченной пластинки. Приобрести навык моделирования задач теплопроводности и решения их с помощью ЭВМ

Федеральное агентство по образованию

Государственное образовательное учреждение высшего

профессионального образования

Тульский государственный университет

Кафедра прикладной математики и информатики

Математическое моделирование 

Лабораторная  работа  №2

“Моделирование задачи нахождения стационарного температурного поля неограниченной пластинки”

Выполнил студент группы                       

Принял                                                                       

Тула, 2005г.

Цель работы:

Приобрести навык моделирования задач теплопроводности и решения их с помощью ЭВМ.

Теоретические сведения:

Будем предполагать, что пластина имеет постоянную толщину, теплопроводность и коэффициент теплообмена. Температура внешней среды является постоянной.

При выводе дифференциального уравнения считаем, что температура по толщине пластинки не изменяется. Оси координат х и у расположим в срединной плоскости пластинки. Рассмотрим тепловой баланс элемента пластинки, имеющего размеры dx, dy, h.

Пластина находится в среде, температура которой равна , теплообмен между пластиной и средой определяется зависимостью

,                                                  (1) где q – поток  тепла, уходящего от пластины в окружающую среду, отнесенный к единице длины пластины, b – коэффициент теплообмена, Т – температура пластины.

Количество тепла, протекающее через грань параллелепипеда,  перпендикулярной оси, например Ох, пропорционально промежутку времени Dt (тепловой поток), скорости изменения температуры и площади грани S, т.е.

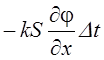, где k – коэффициент теплопроводности. Из курса анализа известно, что значение производной в точке х + Dх будет равно 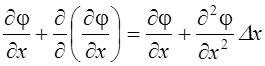 (с точностью до бесконечно малых высшего порядка). Поэтому величина потока, выходящего через грань параллелепипеда, равна .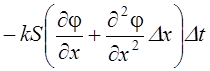

Взяв разность величин входящего и выходящего тепловых потоков, получим количество тепла DQ, сообщенное выбранному участку за время Dt:

.

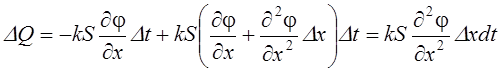Составив условие равенства нулю суммы потоков тепла, проходящих через грани рассматриваемого параллелепипеда, получим

или

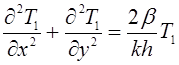, т.е.

,                                                   (4)

где .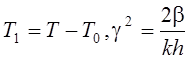

Положим, что пластинка имеет неограниченные размеры, и рассмотрим действие точечного источника. За начало координат примем точку, где находится источник тепла. Область действия источника будет представлять собой окружность с r ® ¥. В этом случае, уравнение примет вид

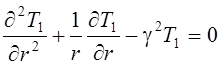.                                           (6)

Граничные условия этой задачи формулируются следующим образом:

1)  Так как в начале координат имеется источник тепла Q, то при r ® 0

;

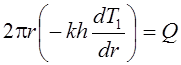2)  В бесконечно удаленной точке = 0 и потому при  .

Решение уравнения (6) имеет вид

;                                             (7)

так как при gr ® ¥ , а , то из условия 2) следует С = 0. Для определения D воспользуемся условием 1):

В силу того, что 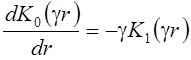, то

.                                         (8)

Но при х ® 0, 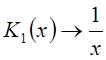, поэтому 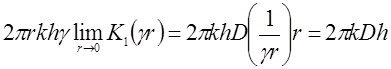. Отсюда получаем 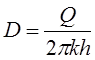, и, следовательно,

.

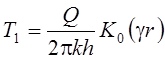Решение задачи в пакете МAPLE 6:

> restart;

> rho1:=7.7;

c1:=0.23;

beta1:=0.3;

> Q:=1300;

k:=3.5;

h:=0.01;

> T:=proc(T0,beta,c,rho,h,r)

local U,a,Gamma;

a:=k/c/rho;

Gamma:=2*beta/a/h;

U:=T0+Q/(2*Pi*a*h)*BesselK(0,Gamma*r);

evalf(U);

end proc:

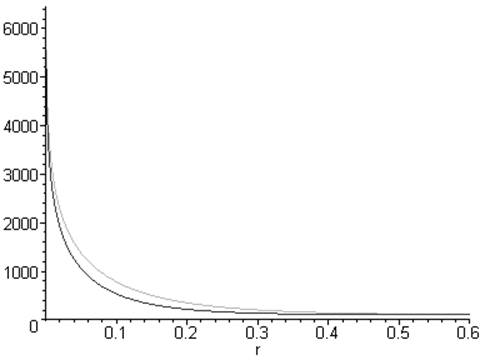
> plot([T(100,1,c1,rho1,.1,r),T(100,0.7,c1,rho1,.1,r)],r=0..0.6);

Рис 1. Зависимость температурного поля от расстояния до источника