Уравнения математической физики. Волновое уравнение для прямоугольника. Вторая краевая задача для однородного уравнения теплопроводности

УРАВНЕНИЯ МАТЕМАТИЧЕСКОЙ ФИЗИКИ

1.  В выражении 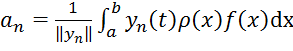функция  означает:

Ответ: Весовую функции (1)

2.  В задачах математической физики имеется:

Ответ: частное решение, удовлетворяющее краевым условиям. (4)

3.  В задаче  какую функцию нужно взять чтобы граничные условия стали однородными:

Ответ:  ()

4.  Волновое уравнение для прямоугольника имеет вид:

Ответ:   (3)

5.  Вторая краевая задача для однородного уравнения теплопроводности имеет решение вида:

Ответ: (3)

6.  В трехмерном пространстве фундаментальным решением уравнения Лапласа является функция: 

Ответ: ()

7.  В уравнении  постоянная  означает: 

Ответ: скорость распространения волн (2)

8.  Выражение есть первая каноническая форма уравнения гиперболического типа. Вторая каноническая форма имеет вид:

Ответ:  (3)

9.  Выражение 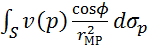 есть: 

Ответ:  Потенциал двойного слоя (3)

10. Для всякого ли линейного однородного уравнения применим метод разделения переменных?  

Ответ: Нет (2)

11. Для определения стационарной температуры в теле необходимо решить:

Ответ: уравнение Лапласа (2)

12. Для определения функции, гармонической внутри круга необходимо решить:

Ответ: уравнение Лапласа(3)

13. Задача  имеет собственное значение:

Ответ:  Задача Штурма-Лиувиля 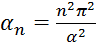 (2)

14. Задача ,  есть задача:

Ответ:  Штурма-Лиувиля (периодическая). ()

15. Задача 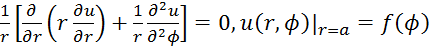 является:

       Ответ: задачей Дирихле для круга (2)

16. Задача  есть задача о распространении тепла:

Ответ:  в шаре (2)

17. Задача  является:

Ответ: задачей Коши для волнового уравнения()

18. Задача   есть:

Ответ: первая краевая задача для волнового уравнения  в круге радиуса (2)

19.  Задача  есть:

Ответ:  смешанная краевая задача для волнового уравнения на отрезке (0,1) (4)

20.  Задача 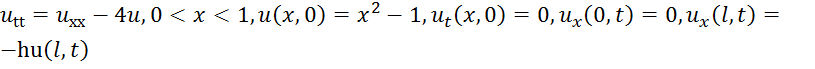есть:

Ответ:  смешанная краевая задача для волнового уравнения (3)

21.  Задача

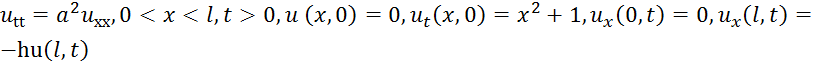есть:

       Ответ: смешанная краевая задача для волнового уравнения ()

22. Задача  есть:

Ответ:  Задача Коши для неоднородного волнового уравнения(4)

23. Задача  есть:

Ответ: вторая краевая задача ()

24. Задача   является:

Ответ: задачей Неймана в кольце  (1)

25.  Задача  является:

Ответ: смешанной краевой задачей для уравнения Лапласа в кольце с радиусами  и  (3)

26.  Задача , в области  есть:

Ответ:  задача Дирихле в квадрате (2)

27. Задача 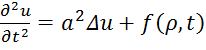 при неоднородных граничных условиях на границе  области  и начальных условиях ,  решается:

Ответ:  сводится к задаче с однородными граничными условиями для чего строится функция , удовлетворяющая граничным условиям ()

28. Задача  при неоднородных граничных условиях на границе области  и начальном условии  решается:

Ответ: сводится к задаче с однородными граничными условиями, для чего подбирается функция , удовлетворяющая граничным условиям и имеющая непрерывные вторые производные (2)

29. Задача корректно поставлена, если:

Ответ: решение существует, единственное и малые изменения исходных данных влекут за собой малые изменения решения()

30. Задача Штурма – Лиувилля сводится к задаче о поиске:

Ответ:  собственных чисел и собственных функций краевой задачи (3)

31. Задача Штурма – Лиувилля является:

Ответ: краевой задачей для обыкновенного дифференциального уравнения (2)

32. Интеграл Пуассона 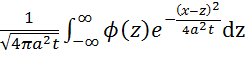является решением задачи:

Ответ: Теплопроводности для бесконечного стержня()

33. Интеграл Пуассона 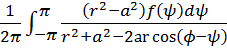есть решение задачи Дирихле:

Ответ:  Для плоского круга()

34. Искомое решение краевой задачи должно удовлетворять:

Ответ: данному уравнению, заданным дополнительным (однородным и неоднородным) условиям (4)

35. Как решается уравнение теплопроводности в случае неограниченного стержня с начальным условием ?

Ответ: По формуле 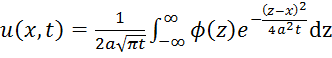 (2)

36. Какой аналитический вид имеет решение уравнения колебания струны, найденное методом Фурье?

Ответ: В виде функции, представленной в форме суммы бесконечного ряда ()

37. Какой вид имеет уравнение теплопроводности для нестационарного случая?

Ответ:   ()

38. Какой вид имеет уравнение теплопроводности для стержня?

      Ответ:   (3) или   (3)

39. Какой вид имеет уравнение теплопроводности для стержня?

Ответ:   (3) или   (3)

40. Каноническая форма линейного уравнения гиперболического типа имеет вид:

Ответ:  (3)