3. ПРАКТИЧЕСКАЯ ЧАСТЬ
1.Критерий Гурвица:
> restart:
with(LinearAlgebra): b0:=17:b1:=19:b2:=34:b3:=2:b4:=34:b5:=2: c0:=22:c1:=9: d4:=b4+c0:d5:=b5+c1:d0:=b0:d1:=b1:d2:=b2:d3:=b3: H1:=d1;
M:=Matrix([[d1,d3],[d0,d2]]);
H2:=Determinant(M,
method=multivar); ![]()
> M := Matrix(3,3,[[d1,d3,d5],[d0,d2,d4],[0,d1,d3]]);
H3:=Determinant(M); ![]()
> M := Matrix([[d1,d3,d5,0],[d0,d2,d4,0],[0,d1,d3,d5],[0,d0,d2,d4]]);
H4:=Determinant(M); ![]()
> M := Matrix([[d1,d3,d5,0,0],[d0,d2,d4,0,0],[0,d1,d3,d5,0],[0,d0,d2,d4,0],[0,0,d1,d3,d5]]);
H5:=Determinant(M);
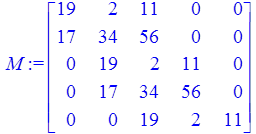
![]()
Полученные результаты говорят о неустойчивости исходной системы.
Подберем параметры таким образом, чтобы система оказалась устойчивой.
> restart:with(LinearAlgebra):
b0:=1: b1:=8: b2:=11: b3:=70: c1:=-5:b4:=30: c0:=-10:b5:=110:
d4:=c0+b4:d5:=c1+b5:d0:=b0:d1:=b1:d2:=b2:d3:=b3: H1:=d1;
>M := Matrix([[d1,d3],[d0,d2]]):
H2:=Determinant(M); ![]()
> M := Matrix(3,3,[[d1,d3,d5],[d0,d2,d4],[0,d1,d3]]):
H3:=Determinant(M); ![]()
> M := Matrix([[d1,d3,d5,0],[d0,d2,d4,0],[0,d1,d3,d5],[0,d0,d2,d4]]):
H4:=Determinant(M); ![]()
> M := Matrix([[d1,d3,d5,0,0],[d0,d2,d4,0,0],[0,d1,d3,d5,0],[0,d0,d2,d4,0],[0,0,d1,d3,d5]]):
H5:=Determinant(M); ![]()
Полученная система устойчива (так как все определители Гурвица положительны).
2.Критерий Михайлова:
> restart:d0:=7: d1:=10: d2:=14: d3:=2: d4:=16: d5:=11:
plot([d1*w^4-d3*w^2+d5,d0*w^5-d2*w^3+d4*w,w=0..1.5]);
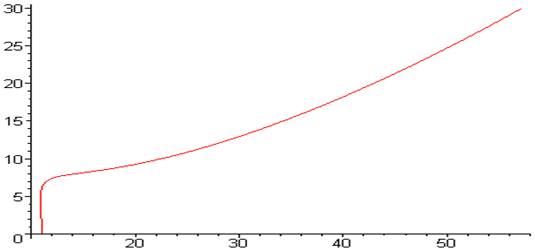
Рис. 1. Кривая Михайлова исходной системы (система неустойчива).
> plot([d1*w^4-80*w^2+100,1*w^5-d2*w^3+25*w,w=0..3.2]);
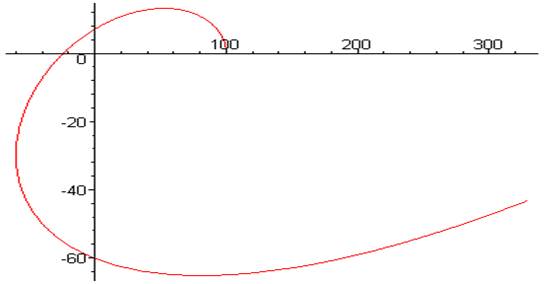
Рис. 2. Кривая Михайлова для устойчивой системы.
> plot([d1*w^4-80*w^2+100,1*w^5-d2*w^3+28*w,w=0..3]);
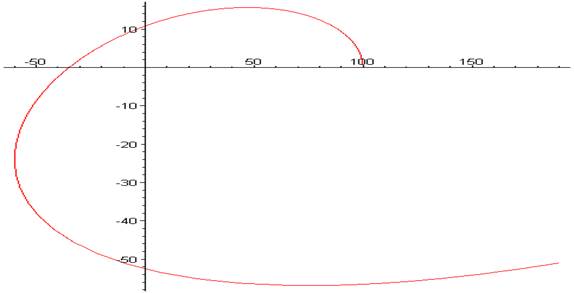
Рис. 3. Кривая Михайлова для системы, находящейся на границе устойчивости.
3.Критерий Найквиста
> restart:d0:=7: d1:=10: d2:=14: d3:=2: d4:=16: d5:=11:
c1:=8:b4:=14: c0:=2:b5:=3:
plot([(c1*(d1*w^4-d3*w^2+b5)+c0*w*(d0*w^5-d2*w^3+b4*w))/((d1*w^4-d3*w^2+b5)^2+(d0*w^5-d2*w^3+b4*w)^2),(c0*w*(d1*w^4-d3*w^2+b5)-c1*(d0*w^5-d2*w^3+b4*w))/((d1*w^4-d3*w^2+b5)^2+(d0*w^5-d2*w^3+b4*w)^2),w=-8..8]);
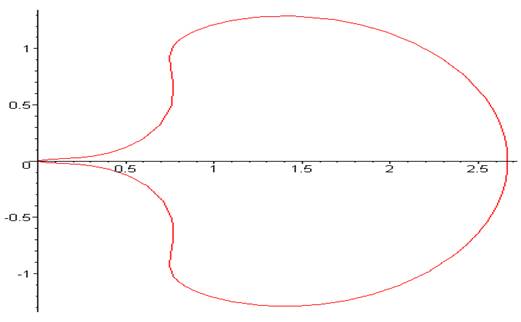
Рис. 4. Амплитудно-фазовая характеристика для исходной системы (согласно критерию Найквиста система неустойчива).
> dn3:=100:b5:=200:c1:=-10:b4:=3:c0:=-5:dn0:=150:
plot([(c1*(d1*w^4-dn3*w^2+b5)+c0*w*(dn0*w^5-2*w^3+b4*w))/
((d1*w^4-dn3*w^2+b5)^2+(dn0*w^5-d2*w^3+b4*w)^2),(c0*w*(d1*w^4-dn3*w^2+b5)-c1*(dn0*w^5-d2*w^3+b4*w))/((d1*w^4-dn3*w^2+b5)^2+(dn0*w^5-d2*w^3+b4*w)^2),w=-11..11]);
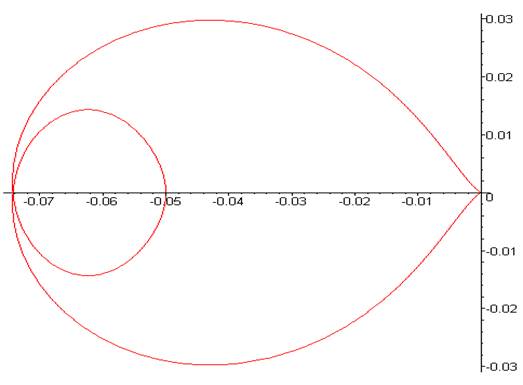
Рис. 5. Амплитудно-фазовая характеристика устойчивой системы (об устойчивости системы судим по критерию Найквиста).
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.