Прогнозирование ряда методом Хольта-Уинтерса. Приобретение навыков краткосрочного прогнозирования экономических показателей методом Хольта-Уинтерса

Министерство образования и науки Российской Федерации

Тульский государственный университет

Кафедра прикладной математики и информатики

СЛУЧАЙНЫЕ ПРОЦЕССЫ

ЛАБОРАТОРНАЯ  РАБОТА  № 7

Прогнозирование ряда методом Хольта-Уинтерса

Выполнил: ст. гр.                                                                         

Проверил: к.т.н., доцент                                                                        

Тула,  2004

1. ЦЕЛЬ РАБОТЫ

Приобретение навыков краткосрочного прогнозирования экономических показателей методом Хольта-Уинтерса.

2. ЗАДАНИЕ НА РАБОТУ

По имеющемуся временному ряду данных () построить прогнозную мультипликативную модель Хольта-Уинтерса и выполнить прогноз на один временной шаг. Необходимо:

1. Оценить начальные значения параметров  и  либо методом наименьших квадратов, либо графически по первым   значениям временного ряда, где  - число точек в периоде (их тоже можно оценить графически).

2. Начальное значение коэффициентов сезонности  () получить делением первых  фактических значений ряда  на их оценки, полученные по линейной модели  ().

3. Параметры адаптации взять , , .

4. По формулам мультипликативной модели Хольта-Уинтерса произвести расчет параметров и оценочных значений показателя (), начиная с .

5. Составить таблицу и графики моделирования.

6. Вычислить средние ошибки расчетов: среднюю арифметическую, среднюю квадратическую, среднюю по модулю.

7. Сделать прогноз ряда на один шаг вперед, т.е. получить значение .

Значения временного ряда представляют собой возврат кредитов банка, выданных на жилищное строительство по кварталам (тыс. р.): 15,1; 18,8; 19,6; 16,0; 16,3; 18,9; 20,5; 17,0; 16,0; 17,1; 19,8; 20,6; 18,0; 19,8; 19,6; 21,0; 19,5.

3. ВЫПОЛНЕНИЕ

1. Построив визуальную картину временного ряда (рис. 1), видим, что число точек, входящих в цикл точно определить нельзя. Однако можем сказать, что их не больше 5.

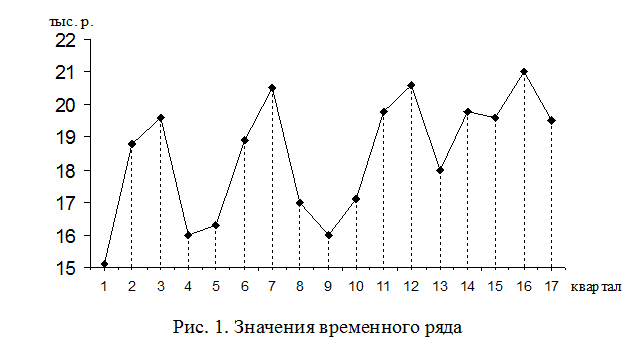
Поэтому для определения числа точек, входящих в период, рассчитаем значения нормированной автокорреляционной функции по формуле

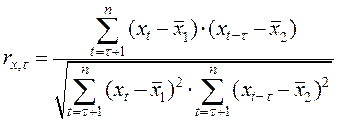, где  ,  .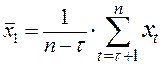

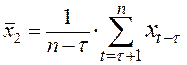В этих формулах возьмем  , .

В результате вычислений получаем

,  ,  ,  ,  ,  .

Таким образом, принимаем число точек в периоде  равным 4.

Оценим значения параметров  и , исходя из условия:

.

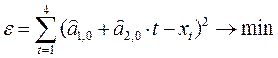Решив систему двух линейных уравнений относительно неизвестных  и , получаем:

,          .

2. Начальное значение коэффициентов сезонности  () вычислим по формуле

.

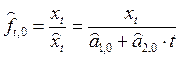Получим

,       ,  

,       .

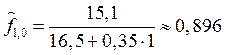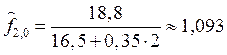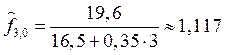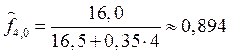3. Произведем расчет параметров , ,  и оценочных значений показателя , используя формулы мультипликативной модели Хольта-Уинтерса:

,

,

,

.

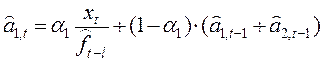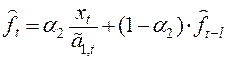Полученные значения запишем в таблицу:

1	15,1	16,325	0,245	0,913434002	14,62953	0,470475	0,031157
2	18,8	17,239	0,3788	1,0915396	18,84263	-0,04263	0,002267
3	19,6	18,21246	0,497732	1,092435429	20,33984	-0,73984	0,037747
4	16	17,89713	0,33512	0,89394062	15,99744	0,002561	0,00016
5	16,3	17,65258	0,219185	0,919400314	16,12447	0,175535	0,010769
6	18,9	18,18023	0,280879	1,06037017	19,84445	-0,94445	0,049971
7	20,5	19,07278	0,403213	1,081872303	20,83578	-0,33578	0,01638
8	17	18,73319	0,254653	0,902064267	16,74636	0,253636	0,01492
9	16	18,09149	0,075382	0,898396256	16,63332	-0,63332	0,039583
10	17,1	17,84681	0,01137	0,999040633	18,92423	-1,82423	0,10668
11	19,8	18,44073	0,127879	1,076975125	19,95051	-0,15051	0,007602
12	20,6	19,17802	0,249762	1,005313361	17,29981	3,300189	0,160203
13	18	18,99945	0,164095	0,927795988	17,06904	0,930965	0,05172
14	19,8	19,35448	0,202282	1,013427564	19,33591	0,464086	0,023439
15	19,6	19,56974	0,204876	1,03171796	21,07612	-1,47612	0,075312
16	21	20,14223	0,2784	1,027676795	20,24925	0,750749	0,03575
17	19,5	20,14444	0,223162	0,951923833	18,68993	0,81007	0,041542

На основании вычисленных значений построим графики исходного временного ряда и ряда, рассчитанного по прогнозной модели (рис. 2).  

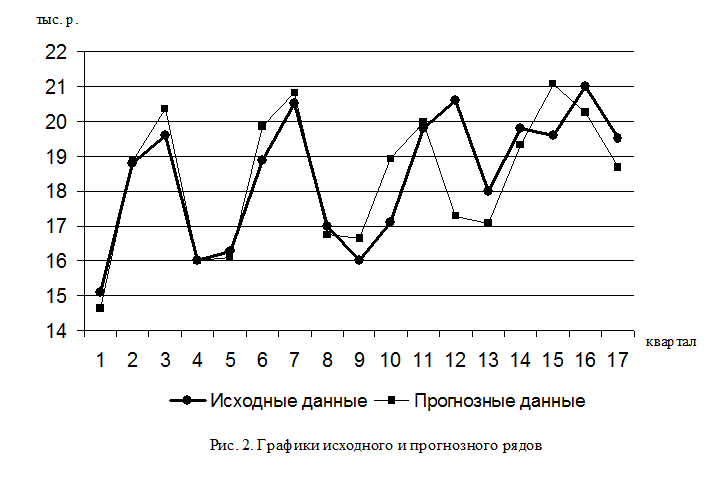
4. Вычислим средние ошибки расчетов:

средняя арифметическая  ;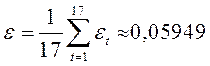

средняя квадратическая   ;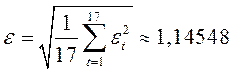

средняя по модулю  .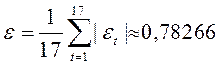

5. Сделаем прогноз на один шаг вперед в момент времени  , используя формулу

.

Получим

 тыс. р.

Таким образом, ожидаемый возврат кредитов банка на следующий квартал равен 20,641 тыс. р.