Математическая модель движения снаряда. Решение системы уравнений

МОСКОВСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ ПУТЕЙ СООБЩЕНИЯ (МИИТ)

ИНСТИТУТ ТРАНСПОРТНОЙ ТЕХНИКИ И СИСТЕМ УПРАВЛЕНИЯ

КАФЕДРА  «ПУТЕВЫЕ, СТРОИТЕЛЬНЫЕ МАШИНЫ И РОБОТОТЕХНИЧЕСКИЕ КОМПЛЕКСЫ»

Индивидуальная (курсовая)  работа  по дисциплине

Математическое моделирование

Вариант №2

Выполнил: студент Герасимов В.А, группа ТНД-111

Принял: Глебова Татьяна Николаевна

МОСКВА 2013

Задача №1.

Математическая модель движения снаряда.

Математическая модель движения снаряда представлена в виде системы уравнений:

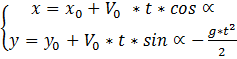  (1)

Где:   – начальные координаты орудия, м;

 – начальная скорость снаряда, по снаряду, м/с;

t – время, прошедшее с момента выстрела, с;

α – угол наклона орудия, по заданию, град;

g – ускорение свободного падения, 9,8 м/

В предложенном примере принимаются значения: =0 и y0=-600.

Тогда система принимает вид:

 

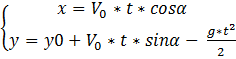
И так, имеется система из двух уравнений с двумя неизвестными:  и t.

Выразим переменную t  из первого уравнения системы:

t=  (2)

и подставим во второе уравнение системы, получив зависимость y=f(x), которая даст возможность построить необходимый график. В результате преобразования можно получить уравнение с одним неизвестным  :

y= * sin -  *   (3)

Приняв определенное значение ( по заданию 55 градусов), следует обратится в Excel, где  нужно выполнить следующие действия:

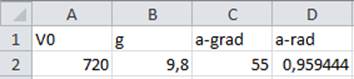
1) поместить в свободные ячейки исходные данные:

=720 ; g=9,8 ;

Угол должен быть выражен в радианах. Для этого нужно воспользоваться передовой формулой: = , где π=3,1416.

При дальнейших расчетах ссылки на эти ячейки должны быть абсолютными( для

2) вычислить следующие параметры:

Т= * sin;                H=*;               L =*sin(2α).

Где: Т- общее время полета снаряда, с;

Н- максимальная высота подъема снаряда, м;

L – дальность полета, м .

Получив значение L, можно начать заполнять ряды x, t и y .

Параметр x будет меняться от 0 до L.Параметры t  и y определяются по соответствующим формулам с использованием абсолютных ссылок для      g и

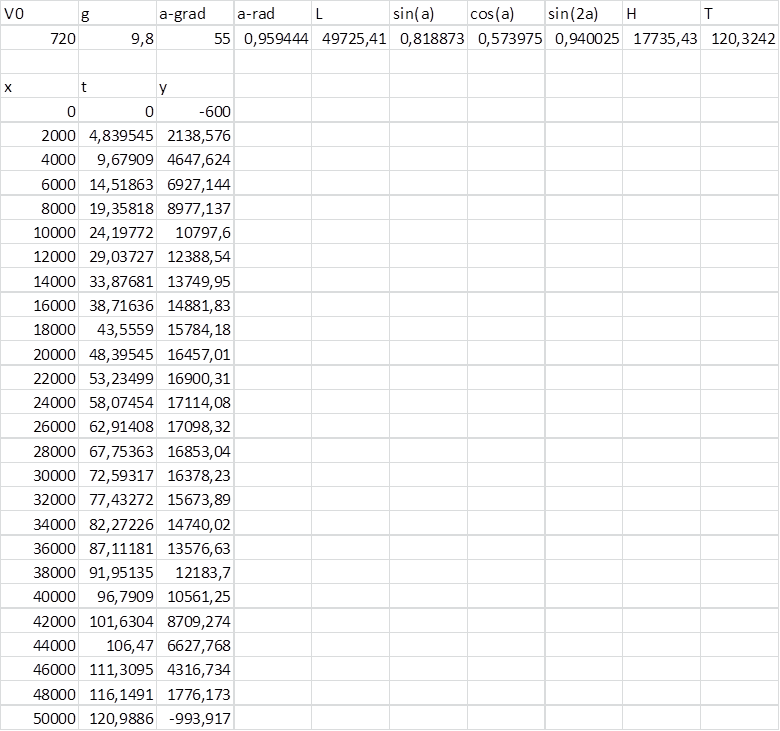
По выделенным столбцам для x и y можно построить точечную диаграмму:

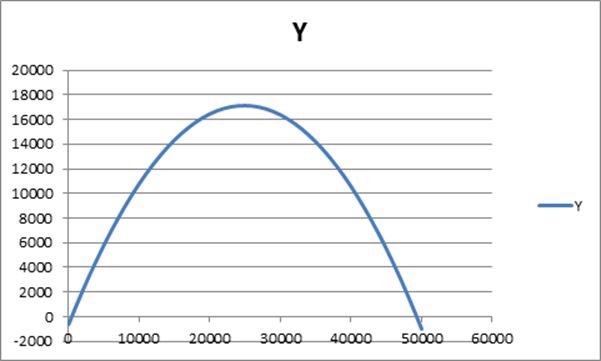
3) выбрать на оси x мишень ( отметить, например, крестиком в 42000м.) и обратиться к «Сервис» - « Подбор параметров». Подобрать подходящий угол стрельбы для « поражения» этой точки .

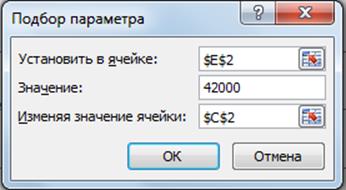
При нажатии кнопки  происходит перерасчет величины

Был угол

a-grad

55

Стал

a-grad

63,75274

График имеет вид

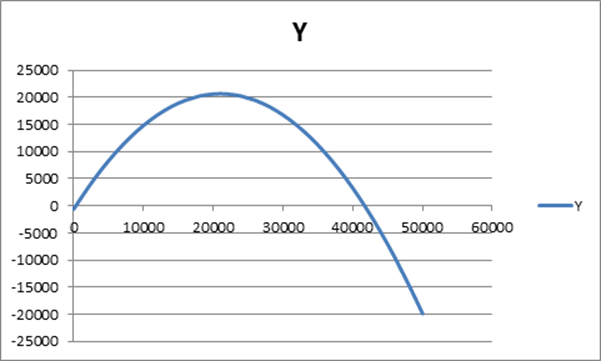
Снаряд попал в заданную цель при значении угла

Задача №2.

Решение системы уравнений.

Найти в Excel все корни системы уравнений:

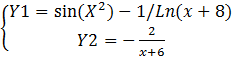   на отрезке [ -5; 5 ].

В Excel выполняем следующие действия:

1)В свободные ячейки добавить значения координаты X в интервале от -5 до 5 с шагом 1 и Y, найденные по-отдельности с помощью 2-х уравнений системы:

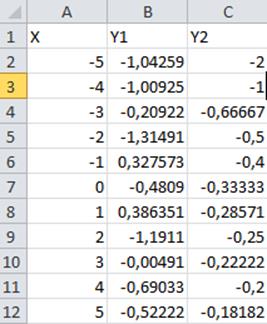
2)По выделенным столбцам для   X  и  Y1,Y2  построить точечную диаграмму:

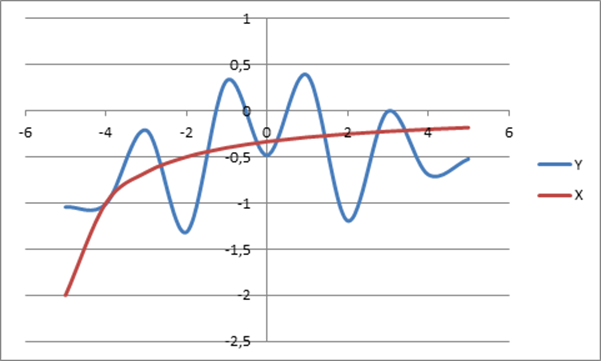
3)Найти разность 2-х уравнений Y2-Y1 и добавить в свободные ячейки:

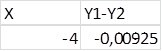
4)Подсчитать количество пересечений 2-х графиков, которые показывают число корней. В данном случае их 8. Затем для каждого отдельного корня примерно (на глаз) определить значение X, добавить это значение в соответствующую ячейку и обратиться к “Сервис”-“подбор параметра” подобрать подходящее значение X при значении

Y2-Y1=0:

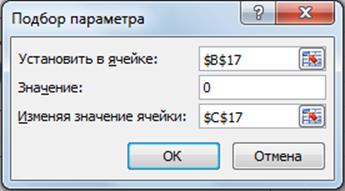
При нажатии кнопки происходит перерасчет величины X, при котором Y2-Y1=0:

Было 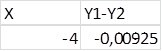, стало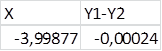

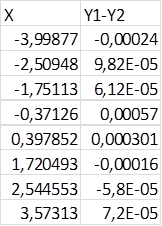
Такую же операцию повторить с остальными семью корнями: