Численное исследование задачи о рассеянии упругих волн неоднородным цилиндром. Порядок численного решения задачи

3.Численное исследование задачи о рассеянии упругих волн неоднородным цилиндром

3.1.  Порядок численного решения задачи

Итак, задача о рассеянии цилиндрических упругих волн неоднородным цилиндром сведена к системе краевых задач для обыкновенных дифференциальных уравнений вида:

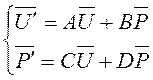 ,                         (1)

где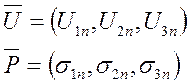                  

при                                                                   (2)

при                                                                             (3)

Данную краевую задачу сведём к решению задач с начальными условиями в соответствии с методом дифференциальной ортогональной прогонки.

Для этого объединим неизвестные функции системы  (1) в вектор  такой, что

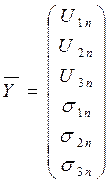,   тогда краевая задача (1),(2),(3) может быть сформулирована следующим образом:

Найти решение системы дифференциальных уравнений 

             , где

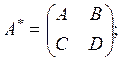
            , где I- единичная матрица.

При начальных условиях  решается задача Коши для системы уравнений  

,

;

верхняя треугольная матрица R определяется равенством

 

Совокупность этих вычислений называют прямым ходом метода прогонки.

В этом методе вектор v(r) при каждом x минимизирует  среди значений нормы y решений системы , удовлетворяющих левому граничному условию.

Так называемый обратный ход метода прогонки заключается в следующем.

Определяется вектор w() размерности - решение системы уравнений   и при заданном  решается в направлении убывания x задача Коши для системы уравнений

                    

Само решение задачи y(x) вычисляется по формуле

Из последнего соотношения при  определим коэффициенты , как значения первых трёх компонентов вектора . Далее полученные значения подставляются в соотношения  для коэффициентов  из п.2.2.2 .Выполнив подобные расчеты для достаточного числа n коэффициентов , получаем возможность приближенно оценить значения потенциалов рассеянных продольных и поперечных волн. Тем самым, определяются поля смещений и напряжений в окружающей среде, порожденные процессом рассеяния упругой волны.  

3.2. Численный анализ полученного решения

После вычислений коэффициентов  становится возможным получить оценку рассеянного поля продольных упругих волн в дальней зоне. В этом случае выражение для потенциала рассеянной волны при   примет вид:

.

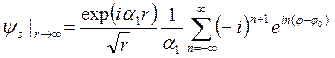Опуская первый множитель, характеризующий распространение ненаправленной цилиндрической волны, и учитывая, что амплитуда падающего поля единичная, получим выражение для нормированной амплитуды потенциала рассеянной волны:

.

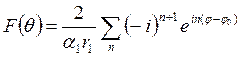В процессе выполнения работы были проведены расчеты зависимости  для некоторых частных видов неоднородностей.

Расчеты проводились для случая, когда внутренняя часть цилиндра представляла собой упругий материал с модулями упругости и плотностью равными: Н/м², Н/м², кг/м³, и двух случаев внешней среды. В первом случае внешняя упругая среда имела характеристики близкие к свойствам идеальной жидкости, а во втором случае ее характеристики совпадали с характеристиками внутренней части цилиндра. Заметим, что параметры , ,  соответствуют средним значениям соответствующих параметров алюминия.  Соответствующие характеристики для неоднородного включения выбирались в виде зависимости:

, где  параметры  Н/м² ,  Н/м²,  кг/ м³ соответствуют средним значениям параметров стали.

Рассматривались два вида линейной зависимости  f(r)  от  r  на отрезке  [r₂, r₁]:

(1)               ;

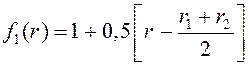  (2)             .

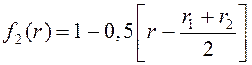
При этом среднее значение функции  f(r)  на отрезке [r₂, r₁] полагалось равным единице. Так как f(r) изменяется линейно, то и соответственно параметры неоднородного включения будут изменяться линейно с размахом 0.5, 0.5, 0.5. Зависимость функции  f(r) от расстояния r от оси цилиндра представлена на

рис.2

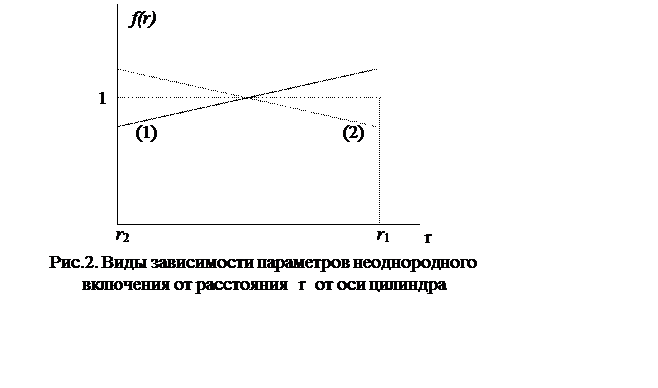Таким образом, в случае зависимости вида  значение изменяющегося параметра неоднородного слоя на границе на 25% меньше соответствующего усредненного параметра, а на границе раздела сред (r=R) – на 25% больше. В случае зависимости вида , наоборот, большее значение параметра достигается на оси цилиндра, а меньшее – на внешней поверхности.

На процесс рассеяния, оценивались отдельные группы параметров неоднородного включения. Были рассмотрены четыре типа неоднородности:

1-й тип: =, , ;

2-й тип: =, , 

3-ий тип: =, ,

4-ый тип: =, ,

Таким образом, при первом типе неоднородности изменяющимся параметром неоднородного слоя полагалась только плотность, причем ее изменение осуществлялось по зависимости , при втором типе неоднородности плотность изменяется по зависимости модули . При этом для первого и второго типа модули упругости считались постоянными и равными соответствующим усредненным значениям неоднородного включения. В третьем и четвертом случае неоднородности переменными характеристиками упругого слоя являются модули упругости, а плотность в этих случаях считается постоянной.

Так же был рассмотрен случай однородного включения, т.е. =, , . Для каждого типа неоднородности были построены соответствующие графики нормированной амплитуды потенциала рассеянной волны и проведено их сравнение с графиками соответствующими однородному цилиндрическому включению.

На графиках, приведенных на рис.3-18 представлены результаты расчетов величины  для указанных выше типов неоднородности цилиндра для первого случая внешней среды. На каждом рисунке сплошной линией представлена кривые, соответствующие характеристикам, полученным для неоднородного упругого включения, пунктирной линией представлена форма рассеяния продольной волны от цилиндра радиусом r₁ , что соответствует случаю однородного включения.