ГЕОМЕТРИЯ И АЛГЕБРА
1. ![]() если и только если
если и только если
Ответ: ![]() - нулевое (3)
- нулевое (3)
2. 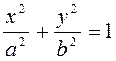 является
является
Ответ: эллипсом или эллиптическим цилиндром (?)
3. а = (1, -1,3),
b = (-2, 2,1), с= (3, -2,5). Смешанное произведение ![]() равно
равно
Ответ: -7 (1)
4. Бесконечная система векторов называется линейно-зависимой, если
Ответ: существует конечная линейно зависимая подсистема ее векторов (2)
5. В ![]() обратным для
обратным для ![]() является
является
Ответ: число
![]()
6. В кольце ![]() обратным для
обратным для ![]() является
является
Ответ: число ![]() (1)
(1)
7. Вектор ![]() в пространстве C комплексных чисел над полем R в базисе
в пространстве C комплексных чисел над полем R в базисе 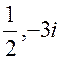 имеет координаты
имеет координаты
Ответ: (16,-3) (?)
8. Верно ли, что всякая квадратная матрица подобна треугольной
Ответ: да (?)
9. Верно ли, что характеристическое уравнение симметричного оператора имеет лишь действительные корни?
Ответ: да (1)
10. Дана точка М(2, —1,1) и плоскость 5х — Зу + z — 18 = 0.
Ответ: точка M и начало координат лежат по одну сторону от плоскости (1)
11. Двусторонний гиперболоид имеет уравнение
Ответ: 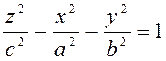 (?)
(?)
12. Для матрицы 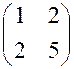 обратной является матрица
обратной является матрица
Ответ: 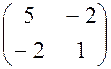 (?)
(?)
13. Для того чтобы система линейных уравнений была совместной, необходимо и достаточно, чтобы
Ответ: ранг матрицы равнялся рангу расширенной матрицы (2)
14. Единичная матрица — это
Ответ: квадратная матрица, по диагонали которой идут 1, а остальные элементы 0 (?)
15. Если в линейно-зависимой системе поменять местами два вектора, то
Ответ: система останется линейно – зависимой (2)
16. Если в нулевой линейной комбинации не все коэффициенты равны нулю, то
Ответ: система линейно зависима (2)
17. Если в
определителе 3-го порядка элементы 1-й строки умножить на ![]() , 2-й на
, 2-й на ![]() , 3-й на
, 3-й на ![]() , то
, то
Ответ: умножится на ![]() (2)
(2)
18. Если в определителе 3-го порядка к элементам 1-й строки прибавить элементы второй, то
Ответ: значение определителя не изменится (?)
19. Закон инерции квадратичных форм утверждает, что
Ответ: одну и ту же квадратичную форму можно привести к каноническому виду различными способами, но число слагаемых с положительным коэффициентами, так же как и число слагаемых с отрицательными коэффициентами, во всех случаях будет неизменно (?)
20. Какое из множеств с обычной операцией умножения является группой: М={1}, S ={-1,1}.
Ответ: ![]() и
и ![]() (3)
(3)
21. Какое из этих утверждений верно?
Ответ: поле комплексных чисел алгебраически замкнуто (3)
22. Какое утверждение верно?
Ответ: всякий линейный оператор, действующий в комплексном линейном пространстве, имеет по крайней мере один собственный вектор (2)
23. Какое утверждение верно?
Ответ: симметричный линейный оператор в любом ортогональном базисе имеет симметричную матрицу (2)
24. Каноническое уравнение гиперболы — это уравнение
Ответ: 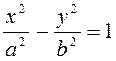 (2)
(2)
25. Каноническое уравнение гиперболического параболоида — это уравнение
Ответ: 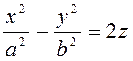 (3)
(3)
26. Каноническое уравнение параболы — это уравнение
Ответ: ![]() (3)
(3)
27. Каноническое уравнение эллипса — это уравнение
Ответ: 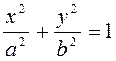 (?)
(?)
28. Квадратичной
формой от переменных ![]() называется
называется
Ответ: всякий однородный многочлен 2 степени этих переменных (2)
29. Корневое
подпространство матрицы 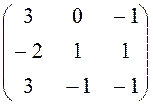 имеют размерности
имеют размерности
Ответ: 3 (3)
30. Корневое
подпространство матрицы 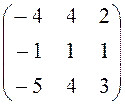 имеют размерности
имеют размерности
Ответ: 2,1 (2)
31. Критерий Сильвестра утверждает, что квадратичная форма положительно определена тогда и только тогда, когда
Ответ: все главные миноры ее матрицы положительны (3)
32. Линейный оператор А : Х —>У однозначно определяется
Ответ: образами базисных векторов пространства X (3)
33. Линейное пространство Х является прямой суммой своих подпространств Y и Z тогда и только тогда, когда
Ответ: базис пространства X есть объединение базисов Y и Z (4)
каждый вектор ![]() единственным образом представим в виде
единственным образом представим в виде ![]()
![]() (2)
(2)
34. Линия второго
порядка ![]() тогда и только тогда имеет
единственный центр, когда
тогда и только тогда имеет
единственный центр, когда
Ответ: 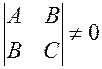 (?)
(?)
35. Любая ортогональная система ненулевых векторов евклидова подпространства
Ответ: линейно независима (является базисом пространства) (?)
36. Матрицы А и В
Ответ: если подобны,то эквивалентны (2)
37. Матрицей квадратичной формы может быть
Ответ: любая симметричная матрица (?)
38. Матрица называется ортогональной, если
Ответ:![]() (2)
(2)
39. Матрица называется симметричной, если
Ответ:![]() (?)
(?)
40. Матрица преобразования координат при переходе от одного базиса к другому
Ответ: всегда не вырождена (2)
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.