41. Множество ![]() относительно умножения
относительно умножения
Ответ: является группой (?)
42. Множество R \ {0} относительно умножения
Ответ: абелева группа (?)
43. Множествовсех квадратных матриц одного и того же порядка относительно операций сложения и умножения образует
Ответ: кольцо (?)
44. Множество всех матриц вида m х n с элементами из поля Р относительно матричного сложения образует:
Ответ: абелеву группу (2)
45. Множествовсех невырожденных матриц одного и того же порядка относительно матричного умножения образует:
Ответ: группу (4)
46. Множество линейных операторов, действующих в линейном пространстве Х относительно операции сложения и умножения всегда являются
Ответ: кольцом (2)
47. Множество матричных многочленов, соответствующих квадратной матрице А образует относительно сложения и умножения
Ответ: ассоциативное, коммутативное кольцо с единицей (4)
48. Неравенство
Коши - Буняковского для векторов ![]() и
и ![]() обращается в равенство тогда и только тогда, когда
обращается в равенство тогда и только тогда, когда
Ответ: эти векторы коллинеарны (?)
49. Обратная матрица существует
Ответ: для любой невырожденной матрицы (2)
50. Объем
параллелепипеда, построенного на векторах ![]() ,
, ![]() ,
, ![]() - равен:
- равен:
Ответ: 51 (?)
51. Окружность — это частный случай
Ответ: эллипса (3)
52. Оператор А: Х —> Х представим в виде прямой суммы операторов В и С тогда и только тогда, когда Х представимо в виде
Ответ: прямой суммы инвариантных относительно A подпространств (1)
53. Определитель произведения двух невырожденных квадратных матриц одинакового порядка
Ответ: отличен от нуля (3)
54. Пара пересекающихся прямых определяется уравнением
Ответ: ![]() (?)
(?)
55. Плоскость Ах+Ву+Зz—5
= 0 перпендикулярна к прямой 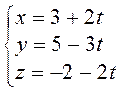 при
при
Ответ: ![]() (?)
(?)
56. Площадь
параллелограмма, построенного на векторах ![]() ;
;![]() , равна:
, равна:
Ответ: 9 (?)
57. Поверхность вращения параболы у2 = 2рх вокруг ее оси симметрии имеет уравнение
Ответ: ![]() (?)
(?)
58. При последовательном выполнении преобразований координат с матрицами Р и R матрица результирующего преобразования S равна
Ответ: S=P∙R (4)
59. При умножении линейных операторов их матрицы
Ответ: перемножаются (?)
60. Прямая 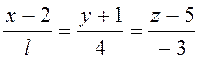 перпендикулярна к плоскости 3x - 2у + Сz + 1 = 0 при
перпендикулярна к плоскости 3x - 2у + Сz + 1 = 0 при
Ответ: ![]() ( )
( )
61. Пусть ![]() , матрицей преобразования координат может быть
, матрицей преобразования координат может быть
Ответ: невырожденная квадратная матрица порядка m (3)
62. Пусть А — матрица, имеющая n строк и m столбцов, n > m. Тогда
Ответ: эти ранги равны (3)
63. Пусть ![]() — корень кратности
— корень кратности ![]() , характеристического многочлена
оператора А. Корневое подпространство
, характеристического многочлена
оператора А. Корневое подпространство ![]() — это
— это
Ответ: ядро оператора ![]() (2)
(2)
64. Работа,
произведенная силой ![]() , когда ее точка приложения
перемещается из начала в конец вектора
, когда ее точка приложения
перемещается из начала в конец вектора ![]() равна
равна
Ответ: 17 (1)
65. Размерность
пространства решений системы ![]() равна
равна
Ответ: 3 (?)
66. Размерность
пространства решений системы ![]() равна
равна
Ответ: 3 (?)
67. Размерность
ядра линейного оператора, заданного матрицей 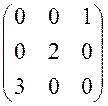 равна
равна
Ответ: 0 (1)
68. Размерность
ядра линейного оператора, заданного матрицей 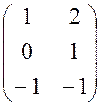 равна
равна
Ответ: 0 (?)
69. Рангом матрицы называется
Ответ: наивысший порядок r отличных о нуля миноров матрицы А (?)
70. Система линейных однородных уравнений совместна, если
Ответ: всегда (а имеет единственное решение, если определитель равен 0) (?)
71. Система собственных векторов соответствующих попарно различным
собственным значениям
Ответ: всегда линейно независима (1)
72. Следующие
линии второго порядка являются центральными: 1) 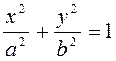 ;
2)
;
2) 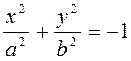 ; 3)
; 3) 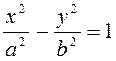 ; 4)
; 4) ![]() ; 5)
; 5) ![]() ; 6)
; 6) ![]() ; 7)
; 7) ![]() ; 8)
; 8) ![]() ; 9)
; 9) ![]()
Ответ:1, 2, 3,4,5 (?)
73. Следующие
линии второго порядка не являются центральными: 1) 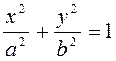 ;
2)
;
2) 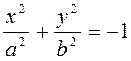 ; 3)
; 3) 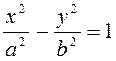 ; 4)
; 4) ![]() ; 5)
; 5) ![]() ; 6)
; 6) ![]() ; 7)
; 7) ![]() ; 8)
; 8) ![]() ; 9)
; 9) ![]()
Ответ: 5,6, 7, 8,9 ( )
74. Теорема
Гамильтона-Кэли утверждает, что если ![]() — характеристический многочлен оператора А, то
— характеристический многочлен оператора А, то
Ответ:![]() (4)
(4)
75. Точка, симметричная точке (1,2,3) относительно плоскости 2x - Зу + 5z - 68 = 0 имеет координаты
Ответ: (7,-7,18) (?)
76. Умножение А ∙В матриц определено
Ответ: для матриц А и В таких, что число столбцов матрицы А равно числу строк матрицы В (3)
77. Уравнение ![]() определяет
определяет
Ответ: на плоскости параболу, в пространстве параболический цилиндр (3)
78. Фундаментальная система решений однородной системы линейных уравнений, это
Ответ: базис подпространства решений (3)
79. Число 1, стоящее на k-ом месте перестановки элементов 1,2,...,n образует
Ответ: k-1 инверсия (2)
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.