





Направление вектора при этом можно выбирать произвольно, но целесообразно его принимать исходящим из неподвижных точек, если они имеются в структуре механизма. В общем случае уравнение замкнутости контура выглядит следующим образом:
n
![]() ∑li =
0, (1) i=1
∑li =
0, (1) i=1
![]() где
li – вектор, соответствующий
i-ому звену, входящему в рассматриваемый контур;
где
li – вектор, соответствующий
i-ому звену, входящему в рассматриваемый контур;
n – число векторов, входящих в контур.
При составлении уравнения замкнутости можно произвольно
выбирать на![]() правление
обхода контура, но в уравнении (1) вектор li записывается со знаком "+", если
его направление совпадает с направлением обхода, и со знаком "–", если
оно противоположно. Структурный и геометрический синтез механизмов на основе обобщённых
структурных модулей подробно изложен в лекции. Далее изложены алгоритмы определения
кинематических параметров для обобщенных структурных модулей при частных значениях
некоторых параметров и приведены примеры решения для конкретных рычажных механизмов:
привода конвейера и долбёжного станка.
правление
обхода контура, но в уравнении (1) вектор li записывается со знаком "+", если
его направление совпадает с направлением обхода, и со знаком "–", если
оно противоположно. Структурный и геометрический синтез механизмов на основе обобщённых
структурных модулей подробно изложен в лекции. Далее изложены алгоритмы определения
кинематических параметров для обобщенных структурных модулей при частных значениях
некоторых параметров и приведены примеры решения для конкретных рычажных механизмов:
привода конвейера и долбёжного станка.
2. Условный механизм первого класса
 В большинстве механизмов
входными звеньями, определяющими движение остальных, являются звенья, совершающие
вращательное движение относительно неподвижной точки. Частный случай условного обобщенного
модуля такой группы представлен на рис. 19. Согласно классификации Ассура – Артоболевского
эта группа звеньев называется условным механизмом первого класса с вращательным
движением входного звена. Обозначим его – I1(0, 1), где в круглых скобках обозначены номера
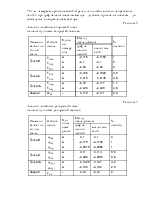
звеньев: 0 – стойка, 1 – кривошип. На рис. 1 это звено S1AB. Для
составления уравнений необходимо выбрать произвольно систему
координат хOу. Уравнение замкнутости векторного контура OABO
для опреде ления
параметров точки B обобщенного структурного модуля I1(0, 1) (рис. 19) с учётом
уравнения (27) будет иметь вид:
В большинстве механизмов
входными звеньями, определяющими движение остальных, являются звенья, совершающие
вращательное движение относительно неподвижной точки. Частный случай условного обобщенного
модуля такой группы представлен на рис. 19. Согласно классификации Ассура – Артоболевского
эта группа звеньев называется условным механизмом первого класса с вращательным
движением входного звена. Обозначим его – I1(0, 1), где в круглых скобках обозначены номера
звеньев: 0 – стойка, 1 – кривошип. На рис. 1 это звено S1AB. Для
составления уравнений необходимо выбрать произвольно систему
координат хOу. Уравнение замкнутости векторного контура OABO
для опреде ления
параметров точки B обобщенного структурного модуля I1(0, 1) (рис. 19) с учётом
уравнения (27) будет иметь вид:
![]()
rA +
l1 −
rB =
0 (2) или (в проекциях на оси Ox и Oy):
x B = x A + l1 ⋅ cos ϕ 1 ,
Для определения аналогов линейных скоростей и ускорений точки B необходимо продифференцировать по параметру ϕ1 уравнения системы (3).
Проекции на оси Oх и Oу аналогов скорости и ускорения точки B опишутся уравнениями:
VϕBx = −l1 ⋅sin ϕ1,
VϕBy = l1 ⋅cos ϕ1; (4)
aϕBx = −l1⋅cosϕ1,
aϕBy = −l1⋅sinϕ1. (5)
Кинематические параметры центра масс S1 определяются по тем же уравнениям, что и для точки B, но для контура OAS1O, т. е. в уравнениях (3–5) следует заменить индекс B на S1, длину l1 на c1, угол ϕ1 на угол (ϕ1 + µ1). Получим уравнения:
rA +
c1 +
rS1 =
0; (6)
xS1 = xA +c1⋅cos (ϕ1 +µ1),
yS1 = yA + c1⋅sin (ϕ1 +µ1); (7)
VϕS1x = −c1 ⋅sin (ϕ1 + µ1),
aϕS1x = −c1⋅cos (ϕ1 +µ1),
aϕS1y = −c1⋅sin (ϕ1 +µ1). (9)
 В случае поступательно
движущегося входного звена I2 (0, 1) (рис. 20) для входной точки B должны
быть заданы ее координаты, аналоги скоростей и ускорений в проекциях на оси Ox
и Oy в любой момент исследуемого отрезка времени или пути. Аналоги скоростей
и ускорений точки S1 и точки B одинаковы, а координаты
центра масс можно определить по уравнениям:
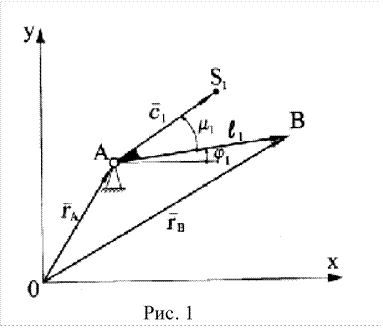
В случае поступательно
движущегося входного звена I2 (0, 1) (рис. 20) для входной точки B должны
быть заданы ее координаты, аналоги скоростей и ускорений в проекциях на оси Ox
и Oy в любой момент исследуемого отрезка времени или пути. Аналоги скоростей
и ускорений точки S1 и точки B одинаковы, а координаты
центра масс можно определить по уравнениям:
xS1 = xB + c1⋅cos(µ1 +µ0),
yS1 = yB +c1⋅sin(µ1 +µ0). (10)
Рис. 2
4.
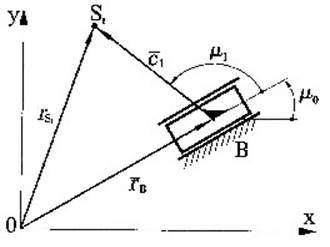
2. Обобщённый модуль второго класса второго вида
Обобщенный модуль этой группы (упрощённый вариант без дополнительных точек), используемый для вывода алгоритмов, представлен на рис. 2. Точка C находится на пересечении линии звена DC и направляющей, по которой перемещается ползун. Уравнение замкнутости контура OBDCO:
![]()
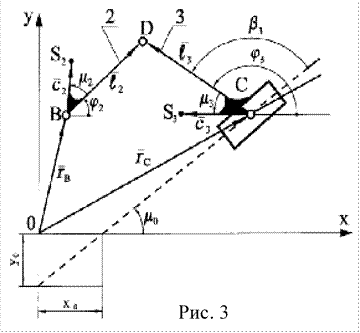
rB +
l2 −l3 −
rC =
0. (11)
В проекциях на оси Ox и Oy:
xyCC == xyBB ++ll22⋅⋅cossin jj 22 −−ll33 ⋅⋅sincosjj 33,, (12)
где ϕ3 = µ0 +β3 (µ0 – угол накло-
на направляющей ползуна CD; β3 – угол между направляющей и вектором длины ползуна).
Кроме уравнения (12) используем уравнение связи между координатами точки С:
yC = (xC − x0 )⋅tg µ0 . (13)
Угол ϕ2 определяется по формуле:
![]() − B ± B2 −4⋅ A⋅C
− B ± B2 −4⋅ A⋅C
cosj 2 = (14)
2⋅ A
где A=a2 +1; B = 2⋅a⋅b; C = b2 −1. (15)
a 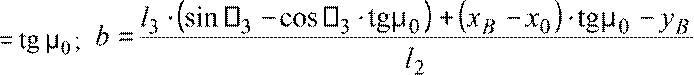 . (16)
. (16)
Если µ0 = 0 или µ0 = 180º, то yC = const, и угол ϕ2 определяется из второго уравнения системы (12):
sinϕ2 = l3 ⋅sin ϕ3 + yC − yB . (17)
l2
При µ0 = 90º или µ0 = 270º ( xC = const) угол ϕ2 определяется из первого уравнения системы (12):
cosϕ2 = l3 ⋅cosϕ3 + xC − xB . (18)
l2
Аналоги скоростей и ускорений звена 2 и точки C можно определять по следующим зависимостям:
|
VϕCx VϕCy |
= VϕBx − l2 ⋅ ωϕ2 ⋅ sin ϕ 2 , = VϕBy − l2 ⋅ ωϕ2 ⋅ cos ϕ 2 ; |
(19) |
|
|
VϕCy = VϕCx ⋅tgµ0 ; |
(20) |
||
|
ω = |
VϕBx ⋅ tgµ0 − VϕBy |
(21) |
|
|
ϕ2 |
|||
l2 ⋅ (sin ϕ2 ⋅ tgµ0 + cos ϕ2)
aϕCx = aϕBx − l2 ⋅εϕ2 ⋅sin ϕ2 − l2 ⋅ ωϕ22 ⋅cos ϕ2 , aϕCy = aϕBy + l2 ⋅εϕ2 ⋅cos ϕ2 − l ⋅ω2 ⋅sin ϕ2 ; (22)
2 ϕ2
aϕCy = aϕCx ⋅tg µ0; (23)
εϕ2 = aϕBx ⋅tg µ0 −l a⋅ϕ(Bysin+ϕl22 ⋅⋅tgωϕ2 µ20(sin+ cosϕ2 ϕ−2cos) ϕ2 ⋅tg µ0) (24)
2
Кинематические параметры точек D, S2иS3определяются по формулам (19–24).
При частных значениях µ0 некоторые выражения существенно упрощаются.
В случае горизонтальной направляющей (µ0 = 0 или µ0 = 180º):
− VϕBy
VϕCy = 0; ωϕ2 = ![]() l ⋅ cos ϕ2 ;
l ⋅ cos ϕ2 ;
2
aϕCy = 0; εϕ2 = ![]() 2 ⋅⋅sincosϕϕ22− aϕBy . (25) l2
⋅
ωϕ2
2 ⋅⋅sincosϕϕ22− aϕBy . (25) l2
⋅
ωϕ2
l2
Для вертикальной направляющей (µ0= 90º или µ0= 270º):
VϕBx
VϕCx = 0; ωϕ2 = ![]() l ⋅sin ϕ2 ;
l ⋅sin ϕ2 ;
2
aϕCx
2
Необходимо выполнить расчёты для заданного угла поворота кривошипа и сравнить с графическим методом. Результаты расчётов проверить, используя систему DINAMIC, занести
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.