Содержание
1. Задание………………………………………………………………………..
2. Обработка статистических данных………………………………………….
2.1 Построение функции распределения……………………………………
2.2 Нормальное распределение……………………………………………...
2.3 Логарифмически нормальное распределение…………………………..
2.4 Закон Вейбулла, при b>1…………………………………………………
3. Теоретические значения вероятностей……………………………………...
4. Показатели долговечности…………………………………………………..
5. Список литературы…………………………………………………………...
Наработка машины до отказа имеет распределение Вейбулла, нормальное, логарифмически нормальное или экспоненциальное.
На испытание поставлены 40-50 машин, а испытания проводятся до их отказа. С использованием вероятностных сеток найти закон распределения случайной величины и определить 80%-ный ресурс машины.
Для 7-го варианта дан следующий статистический ряд случайных величин X, характеризующий число произведенных опытов количеством n = 40:
|
908 |
1249 |
403 |
651 |
2670 |
2080 |
1425 |
1164 |
716 |
822 |
|
640 |
1791 |
749 |
508 |
588 |
582 |
448 |
1358 |
201 |
1618 |
|
1558 |
1288 |
703 |
1205 |
1045 |
1302 |
1111 |
790 |
1261 |
983 |
|
2124 |
328 |
1398 |
1481 |
583 |
609 |
501 |
1144 |
356 |
305 |
Задачи математической статистики состоят в том, чтобы на основании знания некоторых свойств подмножества элементов, взятых из некоторого множества, сделать какие-то утверждения о свойствах этого множества, называемого генеральной совокупностью, т.е. совокупностью объектов, содержащей все исследуемые объекты.
Первичные записи статистических наблюдений за случайной величиной представляют собой простой статистический ряд, в котором записываются номера опытов и значения случайной величины, наблюдавшиеся в этих опытах.
Полученные числовые значения случайной величины располагаются в возрастающем порядке (вариационный ряд). Для возрастающего ряда эмпирическая функция распределения:
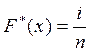 , (1.1)
, (1.1)
По оси абсцисс откладывается
наибольшее значение случайной величины пробега ![]() ч., а
по оси ординат единица. Этими величинами будет ограничен график (рис. 1.1).
ч., а
по оси ординат единица. Этими величинами будет ограничен график (рис. 1.1).
Другим видом обработки первичных
записей опытов, т.е. простого статистического ряда, является поразрядная
группировка полученных из опытов значений случайной величины. Из данных
статистического ряда для непрерывных случайных величин строится гистограмма,
изображающая статистическую плотность распределения. Она позволяет получить
первое представление о виде распределения. Данные вносятся в таблицу 1.2. В ней
отмечаются : разряд и его длина ![]() ,
частота
,
частота ![]() ,
частость
,
частость ![]() , равная
частоте, деленной на общее число наблюдений n, высота разряда
, равная
частоте, деленной на общее число наблюдений n, высота разряда ![]() , равная
частости, деленной на длину разряда (является статистической плотностью
распределения в i-м разряде).
, равная
частости, деленной на длину разряда (является статистической плотностью
распределения в i-м разряде).
Таблица 1.2 – Статистический ряд наработки между отказами машин, ч
|
Номер разряда i |
Разряд |
Длина разряда li |
Частота (число) наблюдений в разряде gi |
Частость p*i = gi / n |
Высота разряда гистограммы f(xi)= (p*i / l)· 10-3 |
|
|
от αi |
до βi |
|||||
|
1 |
0 |
425 |
425 |
5 |
0,125 |
0,294 |
|
2 |
425 |
850 |
425 |
14 |
0,35 |
0,823 |
|
3 |
850 |
1275 |
425 |
9 |
0,225 |
0,529 |
|
4 |
1275 |
1975 |
700 |
9 |
0,225 |
0,321 |
|
5 |
1975 |
2675 |
700 |
3 |
0,075 |
0,107 |
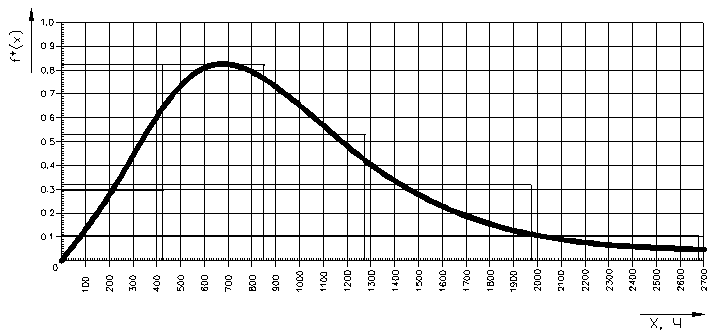
Рисунок 1.2 – Гистограмма наработок до отказа
Полученная гистограмма может отображать появление неисправностей по следующим законам:
· Распределение Вейбулла;
· Нормальное распределение;
· Логарифмически-нормальное распределение.
Поэтому, при невозможности определения закона распределения графически, будем находить закон распределения статистическим методом.
При небольшом числе опытов для определения закона распределения, его параметров, значений гамма-процентного ресурса и вероятности безотказной работы удобно пользоваться вероятностными шкалами.
При построении шкалы F(t) наименьшее и наибольшее значения функции распределения принимаются равными 0,001 и 0,999. Вертикальная шкала неравномерная. При длине вертикальной оси 150 мм, наименьшее значение F(t) равно –75мм, наибольшее 75мм. Горизонтальная шкала равномерная. Масштабный фактор Kt определяется в зависимости от области изменения величины t:
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.