Построение графика статистической функции распределения. Вариационный ряд. Построение гистограммы наработок между отказами

1. Исходные данные:

Наработка до отказа имеет распределение приведенное в таблице 1. Определить гамма-процентный ресурс машины с использованием вероятностных сеток.

Таблица 1 – Наработка до отказа, ч.

429	1624	1371	292	196	645	995	1869	995	2730
1124	178	203	1393	638	894	1833	1690	921	929
1284	884	595	1719	212	614	1742	1193	133	1452
634	420	742	696	1447	1383	551	214	364	762

2. Построение графика статистической функции распределения

Удобным способом получить представление о распределении случайной величины Х является построение графика статистической функции распределения выборки (х₁, … х_n).

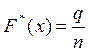,                                                                                                                  (1)

где q – число опытов, в которых случайная величина Х принимала значения меньше х;

n – общее число произведенных опытов.

Статистический ряд перестраивается так, чтобы полученные числовые значения случайной величины располагались в возрастающем порядке (вариационный ряд).

Для возрастающего ряда эмпирическая функция распределения записывается:

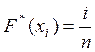 ,                                                   (2)

где i – порядковый номер опыта.

Таблица 2 – Вариационный ряд

i*	1	2	3	4	5	6	7	8	9	10
li	133	178	196	203	212	214	292	364	420	429
i/n	0,025	0,05	0,075	0,1	0,125	0,15	0,175	0,2	0,225	0,25

11	12	13	14	15	16	17	18	19	20
551	595	614	634	638	645	696	742	762	884
0,275	0,3	0,325	0,35	0,375	0,4	0,425	0,45	0,475	0,5

21	22	23	24	25	26	27	28	29	30
894	921	929	995	995	1124	1193	1284	1371	1383
0,525	0,55	0,575	0,6	0,625	0,65	0,675	0,7	0,725	0,75

31	32	33	34	35	36	37	38	39	40
1393	1447	1452	1624	1690	1719	1742	1833	1869	2730
0,775	0,8	0,825	0,85	0,875	0,9	0,925	0,95	0,975	1

3. Построение гистограммы наработок между отказами.

Другим видом обработки статистического ряда является поразрядная группировка полученных из опытов значений случайной величины. Из данных статистического ряда для непрерывных случайных величин строится гистограмма, изображающая статистическую плотность распределения. Она позволяет получить первое представление о виде распределения.

Высота разряда:

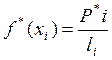;                                                                                                                (3)

где P^*_i – частость;

l_i – длина разряда.

Частость:

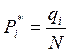,                                                                                                                (4)

где q_i – число наблюдений в разряде (частота).

Длина разряда:

,                                                                                                                (5)

где  - максимальное значение случайной величины в разряде i;

 -  минимальное значение случайной величины в разряде i.

Таблица 3.

Номер разряда i	Разряд		Длина разряда li	Число наблюдений в разряде gi	Частость p*i	Высота разряда f*(xi)·10-3
	от αi	до βi
1	0	400	400	8	0,2	0,5
2	400	800	400	11	0,275	0,69
3	800	1200	400	8	0,2	0,5
4	1200	2000	800	12	0,3	0,38
5	2000	2800	800	1	0,025	0,031

4. Построение графика функции распределения на вероятностной сетке.

Экспоненциальное распределение

Функция распределения случайной величины:

.                                                         (6)

Логарифмируя это выражение, получим линейную зависимость:

.                                                   (7)

Переходим к построению вероятностных шкал F(t).

На горизонтальной оси наносится равномерная шкала t с масштабным фактором K_t :

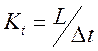.                                                               (8)

На вертикальной оси F(t) наносятся значения –ln [1-F(t)], а надписываются значения F(t). Шкала неравномерная. Наименьшее значение F(t) равно нулю. Наибольшее значение удобно принять равным 0,999. Тогда –ln (1-0,999)=6,908.

При длине вертикальной оси 150 мм,

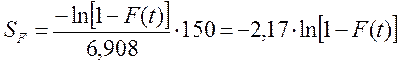.           (9)

Параметр распределения:

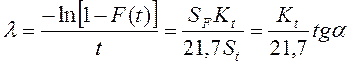.                  (10)

Распределение Вейбула

Функция распределения случайной величины:

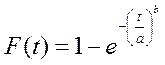.                                                  (11)

Величина S_Fдля вертикальной шкалы длиной 150 мм определяется логарифмированием.

Примем F(t) крайние значения 0,001 и 0,999. Для этих значений размах составит 8,84  (от -6,91 до 1,93).

Числовые значения S_Fприведены в справочнике.

Горизонтальная шкала неравномерная и строится также, как для логарифмически нормального распределения.

Параметр b:

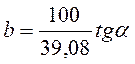.                                                       (12)

Параметр а определяется точкой пересечения найденной прямой с осью t.

Графики на вероятностных сетках представлены на рисунке 3 и рисунке 4.

Полученная гистограмма наработок машины (см. рис. 2) позволяет сделать предположение о том, что наработки между случайными отказами подчиняются закону Вейбула, плотность распределения которого:

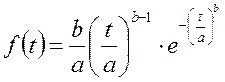                                        (13)

где t – значение случайной величины T (наработка до отказа);

a – параметр масштаба (из графика а=990);

b – параметр формы ().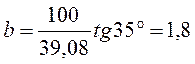

А закон распределения будет иметь вид:

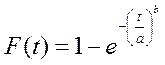                                                   (14)

Вероятность попадания случайной величины в i – й разряд:

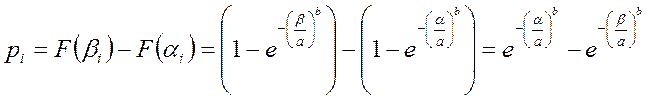              (15)

Подставляя в последнюю формулу а=990 ; b=1,8 и значения α_i и β_iдля каждого разряда из таблицы 3, получим теоретические значения p_i , приведенные в таблице 4.

Таблица 4.- Теоретические значения вероятностей.

Номер разряда, i	Середина разряда,		Теор. вероятность, pi
1	200	1-0,823	0,177	0,003
2	600	0,823-0,508	0,315	0,005
3	1000	0,508-0,246	0,262	0,015
4	1600	0,246-0,029	0,217	0,032
5	2400	0,029-0,0016	0,0274	0,0002

Критерий Пирсона:

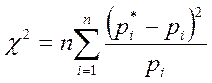;                                         (16)

.

Распределение χ² зависит от параметра r, называемого числом степеней свободы.

r=k-(ψ+1)                                                              (17)

где k – число разрядов статистического ряда (k=5);

ψ – число параметров предполагаемого распределения (ψ=0).

r=5-0-1=4.

По справочнику для χ² =2,2 и r=4 находим вероятность p=0,7358 , что больше 0,05.

Следовательно предполагаемый закон Вейбула не противоречит опытным