![]() , (1.2)
, (1.2)
![]() , (1.3)
, (1.3)
где L – ширина графика, мм;
tmax – наибольшее значение вариационного ряда;
tmin – наименьшее значение вариационного ряда;
![]() ,
,
![]() .
.
График функции распределения показан на рисунке 1.3.
Для логарифмически нормального закона график функции распределения строится так же, за исключением того, что горизонтальная шкала t неравномерная, логарифмическая. График функции распределения показан на рисунке 1.4.
 |
Рисунок 1.3 – График функции логарифмически нормального распределения
Для закона Вейбулла график функции распределения строится так же, как и график логарифмически нормального распределения. График функции распрделения показан на рисунке 1.5.
Числовые значения SF(t) для нормального, логарифмически нормального законов и закона Вейбулла приведены в таблице П.1 приложения. Значения St для логарифмически нормального закона и закона Вейбулла приведены в таблице П.2 приложения.
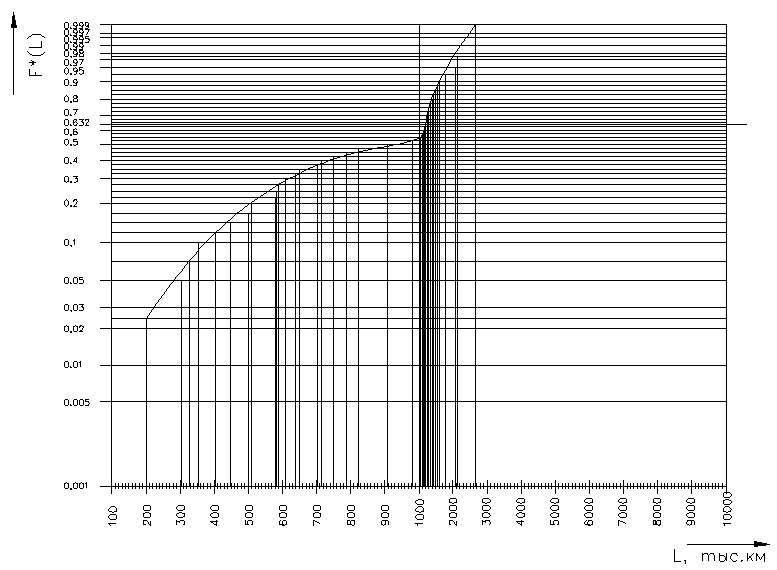 |
Рисунок 1.3 – График функции распределения Вейбулла
Полученные графики функций распределения позволяют сделать вывод о том, что наработки между случайными отказами подчиняются нормальному закону распределения, плотность которого
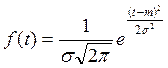 , (3.1)
, (3.1)
где ![]() –
математическое ожидание случайной величины Т,
–
математическое ожидание случайной величины Т,
![]() –
среднее квадратическое отклонение Т.
–
среднее квадратическое отклонение Т.
В вероятностных задачах
математическое ожидание определяют в зависимости от вероятности ![]() появления
значения ti для дискретных величин
появления
значения ti для дискретных величин
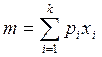 . (3.2)
. (3.2)
где k – число возможных значений случайной величины;
Среднее квадратическое отклонение
![]() . (3.3)
. (3.3)
где D – дисперсия случайной величины, характеризующая ее рассеяния относительно математического ожидания. Для дискретной величины.
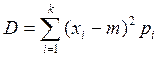 . (3.4)
. (3.4)
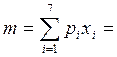 1028,75,
1028,75,
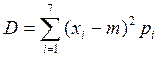 =343126,625,
=343126,625,
![]() .
.
Для нормального закона функции распределения будет иметь вид
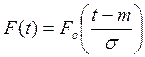 , (3.5)
, (3.5)
где Fo – функция нормированного распределения, числовые значения которой приведены в таблице П.2 приложения [1].
Вероятность попадания случайной величины в i-ый разряд
![]() . (3.6)
. (3.6)
Для случая логарифмически нормального распределения, учитывая (3.5) и полученные значения числовых параметров распределения, формула (3.6) примет вид
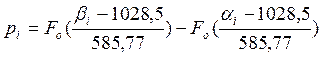 . (3.7)
. (3.7)
Подставляя сюда значения ![]() и
и ![]() для
каждого разряда из таблицы 1.2, получим теоретические значения вероятностей
для
каждого разряда из таблицы 1.2, получим теоретические значения вероятностей ![]() ,
приведенные в таблице 1.3.
,
приведенные в таблице 1.3.
Таблица 1.3 – Теоретические значения вероятностей
|
Номер разряда i |
Середина разряда |
|
Теорет. вероятность |
|
|
1 |
212,5 |
|
0,1123 |
0,0014 |
|
2 |
637,5 |
0,8485 – 0,6217 |
0,2268 |
0,0669 |
|
3 |
1062,5 |
0,6628 – 1 + 0,6217 |
0,2845 |
0,0173 |
|
4 |
1625 |
0,94738 – 0,6628 |
0,28458 |
0,0005 |
|
5 |
2325 |
0,997523 – 0,94738 |
0,050143 |
0,0359 |
Критерий Пирсона
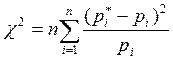 , (3.7)
, (3.7)
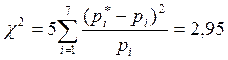 .
.
Число степеней свободы
![]() , (3.8)
, (3.8)
где k – число разрядов статистического ряда,
ψ – число параметров предполагаемого распределения.
Число степеней свободы по (3.8) при числе параметров предполагаемого распределения ψ=2
![]() .
.
Теперь, используя таблицу П.6
приложения [1], для ![]() и
r=2 находим вероятность p=0,2231, что больше 0,05.
и
r=2 находим вероятность p=0,2231, что больше 0,05.
Следовательно, предполагаемый закон не противоречит опытным данным.
Долговечность количественно оценивается с помощью двух групп показателей: ресурса как показателя, связанного с наработкой объекта, и срока службы, связанного с календарной продолжительностью.
Ресурс машины является случайной величиной, поэтому на практике ресурс определяется с заданной вероятностью γ процентов, а гамма-процентный ресурс Тγ находится из уравнения
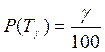 . (3.1)
. (3.1)
Заданный процент объектов – γ-регламентированная вероятность. Гамма-процентный ресурс при нормальном распределении
![]() , (3.2)
, (3.2)
где ![]() – средний ресурс,
определяемый по формуле;
– средний ресурс,
определяемый по формуле;
up – квантиль нормального распределения, определяемая по таблице П.3 приложения [1]. Для 80-% ресурса квантиль up = 0,842.
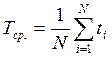 , (3.3)
, (3.3)
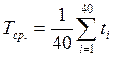 =40646/40=1016,15 ч,
=40646/40=1016,15 ч,
![]() ч.
ч.
1. Каргин В.А, Основы теории надежности и технической диагностики: Учеб. Пособие. – Новосибирск: Изд-во СГУПСа, 2002. – 99 с.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.