Расчет прямоугольного сечения в общем случае действия сил. Усилия, вызывающие только нормальные напряжения

2. Расчет прямоугольного сечения в общем случае действия сил.

В общем случае нагружения в произвольном поперечном сечении стержня внутренние (распределенные) силы  можно свести к шести компонентам внутренних усилий:

- трем усилиям, приложенным к центру тяжести сечения «О» и направленным вдоль координатных осей X, Y, Z.

-трем парам сил, действующим вокруг этих же осей:

Внутренние усилия определяются как алгебраическая сумма проекций всех внешних сил , расположенных по одну сторону от сечения на соответствующие оси.

При -растяжение; при- сжатие.

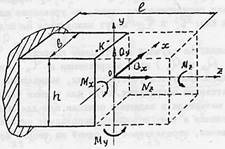
Внутренние усилия определяются как алгебраическая сумма моментов всех внешних сил, расположенных по одну сторону от сечения относительно соответствующих осей.

Величины суммарных напряжений определяют, используя принцип независимости действия сил. Возможны основные комбинации:

1. Усилия, вызывающие только нормальные напряжения, например растяжение- сжатие и поперечные изгибы (без учёта поперечных усилий):

2. Усилия, вызывающие только касательные напряжения, например сдвиг по направлению осей X, Y и кручение вокруг оси Z; тогда по формуле Журавского соответственно

Общее напряжение при сдвиге определяется как геометрическая сумма .

Напряжение при кручении:

Общее касательное напряжение :

3. В большинстве случаев касательное напряжение (от поперечных усилий ) малы в сравнении с и ими пренебрегают. Если потребуется учесть усилия, вызывающие как нормальные, так и касательные напряжения, тогда для оценки несущей способности, прочности материала в заданном сечении или для подбора необходимой площади сечения и тому подобного используют эквивалентное нормальное напряжение, определяемое по одной из теорий прочности и сравниваемое с допускаемым нормальным напряжением при растяжении- сжатии.

3. Совместное действие изгиба и кручения на стержни круглого и кольцевого сечения.

В общем случае действия внешних сил на вал круглого поперечного сечения могут быть представлены следующими деформациями: прямыми поперечными изгибами относительно осей X, Y, кручением относительно продольной оси Z и центральным растяжением или сжатием.

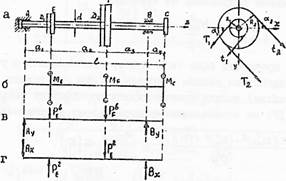
Совместное действие внешних нагрузок представим по принципу независимости действия сил раздельно в виде действия крутящих  моментов и действия сосредоточенных нагрузок, включая и опорные реакции в подшипниках, в вертикальной и горизонтальных плоскостях.

Значения силовых воздействий:

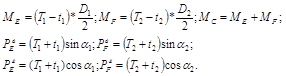
Опорные реакции определим из нагрузок по схемам (в, г). эти схемы воздействия сил на вал используются затем для построения эпюр и при наличии осевых сил .

Эпюры внутренних усилий позволяют определить в опасных сечениях напряжения:

- нормальное от изгибов во взаимно перпендикулярных плоскостях относительно осей X, Y

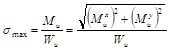
- касательное напряжение от кручения

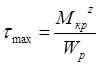
Проверка прочности вала (или подбор его сечения) с учетом одновременного воздействия изгиба и кручения должна производиться по одной из теорий прочности по эквивалентному нормальному напряжению:

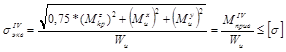
Отсюда требуемое значение ,

Или требуемый

Данная методика применима и к валам кольцевого сечения с учетом особенности площади его сечения.

5. Косой изгиб. Определение нормальных напряжений, положения нейтральной линии, положения плоскости изгиба и величины полного прогиба при косом изгибе.

Косым изгибом называется такой вид деформации, при котором изгибающий момент действует в плоскости, проходящей через ось стержня, но не совпадающей ни с одной из главных центральных осей инерции поперечного сечения.

При косом изгибе направление прогиба не совпадает  с направлением действия внешней силы.

По существу косой изгиб сводится к двум плоским изгибам относительно осей Y и Z.

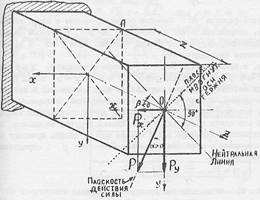
В общем случае изгиба, характеризующимся наличием в сечении «А» балки нормальной силы N в обеих составляющих изгибающего момента, нормальное напряжение в любой точке сечения для правой системы координат σ:

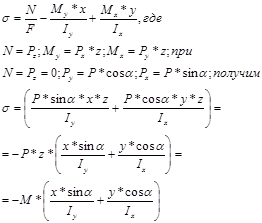
Для определения опасного сечения необходимо при косом изгибе построить эпюру изгибающих моментов, как для плоского изгиба, используя правило знаков для сопротивления материалов. Тогда окончательная формула для σ запишется так:

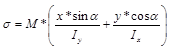
В этой формуле М берется со своим знаком с эпюры изгибающих моментов, координаты точки по осям X и Y, в которой определяется напряжение, берутся со своими знаками. Знак у σ в данной точке получается автоматически.

Если нет необходимости определять знак напряжения в конкретной точке (например, при расчетах балок из пластичных материалов на прочность, у которых ), то при любом направлении координатных осей все члены выражения для берутся со знаком «плюс».

Нейтральная линия в случае косого изгиба проходит через начало координат и составляет с осью ОХ угол β, определяемый следующим образом:

, где угол α откладывается от оси y.

В нашем случае α>0. Угол β откладывается от оси Х.