Теорема Кастильяно и её применение для определения перемещений в стержневых системах. Статически определимые и неопределимые стержневые системы

Статически определимые и неопределимые стержневые системы. Понятия о связях, накладываемых на систему. Геометрически изменяемые и неизменяемые системы. Связи необходимые и дополнительные. Определение степени статической неопределимости. Внешняя и внутренняя статическая неопределимость. Привести примеры.

Геометрическая неизменяемость системы - способность этой системы с одной стороны быть закреплённой, с другой стороны не менять своей конфигурации.

Связь- устройство, ограничивающее одну степень свободы тела как абсолютно твёрдое. Статически неопределимой называют такую систему, которая не может быть рассчитана по методу сечений с использованием лишь одних условий равновесия, так как она обладает лишними связями. Системы, в которых число неизвестных сил внешних и внутренних больше уравнений равновесия называются статически неопределимыми. В таких системах больше связей, чем необходимо для равновесия. В качестве лишних следует принимать те связи, которые необходимо отбросить из состава заданной, чтобы превратить ее в статически определимую и геометрически неизменяемую систему.

Количество лишних связей(дополнительные), которые следует удалить из статически неопределимой системы для обращения ее в статически определимую и геометрически неизменяемую, называют степенью статической неопределимости. Следует различать внешне статически неопределимые и внутренне статически неопределимые системы.

Рис. 2.1

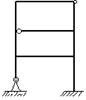
Внешне статически неопределимой называют такую систему, которая имеет только лишние внешние связи, т.е. лишние опорные закрепления. Примером внешне статически неопределимой плоской системы является трехпролетная рама (рис. 2.1).

Степень статической неопределимости системы С легко установить путем вычитания из общего числа опорных стержней m число стержней, необходимых для сохранения геометрически неизменяемого прикрепления системы (одно - для одномерных; три - для плоских и шесть - для пространственных систем).

Для плоской рамы, изображенной на рис. 2.1, учитывая, что защемление эквивалентно трем опорным стержням, получаем:

m = 3 + 2×2 +1 = 8; C = m - 3 = 8-3 = 5, т.е. данная система 5 раз статически неопределима.

Для рам формула будет ССН=С-Н+3*К-Ш,

где С-число наложенных связей (число реакций и моментов во всех реакциях );

Н-кол-во уравнений (одно - для одномерных; три - для плоских и шесть - для пространственных систем).

К- кол-во контуров

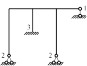Ш- число шарниров (если в углу 1, по средине 2)

ССН=5-3+3*2-3=5

Внутренне статически неопределимой называют систему, обладающую лишними связями, введенными для взаимного соединения частей системы.

Двухопорная рама с затяжкой (рис. 2.2, а) внутренне один раз статически неопределимой. Статически определимая система (рис. 2.2, б) получена из заданной (рис. 2.2, а) путем разрезания затяжки ab. И при этом взаимодействие частей затяжки заменяется только одной неизвестной осевой силой N₁ . Следовательно, в статически определимой системе, изображенной на рис. 2.2, б имеем одно лишнее неизвестное N₁ , которое невозможно определить при помощи метода сечений. Поэтому заданная система (рис. 2.2, а) является один раз статически неопределимой.

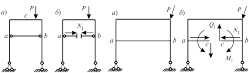
Рис. 2.2                                            Рис. 2.3

Если затяжку жестко заделать в стойки, как это показано на рис. 2.3, а, то получим трижды статически неопределимую систему.

Действительно, в данном случае после разрезания нижнего ригеля ab, взаимодействие частей ac и bc характеризуется уже тремя неизвестными усилиями N₁, Q₁, M₁ (рис. 2.3, б), которые нельзя определить из условия равновесия. Поэтому система, изображенная на рис. 2.3, a является три раза внутренне статически неопределимой.

Отметим следующие основные свойства статически неопределимых систем.

Статически неопределимые системы ввиду наличия добавочных лишних связей, по сравнению с соответствующей статически определимой системой оказывается более жесткой, а при идентичном характере нагружения значения усилий получаются меньшими. Следовательно, и более экономичными. Разрушение лишних связей в нагруженном состоянии, не ведет к разрушению всей системы в целом, так как удаление этих связей приводит к новой геометрически неизменяемой системе, в то время как потеря связи в статически определимой системе приводит к изменяемой системе.

В строительной механике различают следующие два классических метода расчета статически неопределимых систем: метод сил и метод перемещений. При расчете по методу сил основными искомыми величинами являются усилия в лишних связях. Знание усилий в лишних связях позволит по методу сечений, как это было показано в первом разделе учебника, выполнять полный расчет по определению усилий, возникающих в поперечных сечениях элементов заданной системы.

20.Метод сил для раскрытия статической неопределимости. Основная и эквивалентная системы. Уравнения перемещений.

Суть этого метода заключается в том, что заданная статически неопределимая система освобождается от дополнительных связей как внешних, так и внутренних, а их действие заменяется соответствующими силами и моментами. Их величины, в дальнейшем, подбираются так, чтобы перемещения системы соответствовали тем бы ограничениям, которые на нее накладываются отброшенными связями.

1) Определение степени статической неопределимости для того, чтобы