Расчет прямоугольного сечения в общем случае действия сил. Усилия, вызывающие только нормальные напряжения, страница 4

Это означает, что для того, чтобы стержень сохранял криволинейную форму, необходимо, чтобы сила Р принимала определенное значение. Наименьшая сила Р, отличная от нуля, будет при n=1

Эта сила называется первой критической или эйлеровой силой. При n=1 имеем:

Уравнение упругой линии примет вид:

Стержень изгибается по половине синусоиды с максимальным прогибом С₁

При любом целочисленном значении n:

и упругая линия стержня изображается кривой в виде n полуволн.

Формула Эйлера верна только при малых прогибах. Если это уравнение написать точно, то получим:

При силе Р больше критической, перемещения растут настолько быстро, что пренебрегать величиной y’² в знаменателе нельзя.

9. Критические напряжения по Эйлеру. Гибкость стержня. Формула Ясинского для стержней средней гибкости. Условие устойчивости. Коэффициент уменьшения допускаемого напряжения.

Различают устойчивые и неустойчивые формы равновесия упругих систем. Сила Р, которая переводит систему из устойчивого в неустойчивое положения равновесия, называется критической.

Эту силу, для центральносжатых стержней , определяют из условия того, что наряду с прямолинейной формой равновесия стержня возможна, при сколь угодно малых отклонениях, криволинейная форма его равновесия.

Критическую силу подсчитывают по формуле Эйлера:

, где

Е- модуль упругости материала;

I_min- минимальный момент инерции сечения (относительно этой оси стержень теряет свою устойчивость);

μl- расчетная или приведенная длина стержня;

μ- коэффициент длины, зависящий от способов закрепления концов стержня. Значение коэффициентов μ для некоторых закреплений стержней приведены на рисунке:

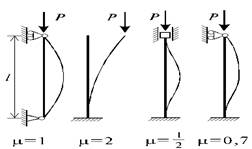
Критическим напряжением называется нормальное напряжение в поперечном сечении центральносжатого стержня, вызванное критической силой:

где λ – гибкость стержня, определяемая по формуле:

i_min – минимальный радиус инерции поперечного сечения стержня.

При выводе формулы Эйлера предполагалось, что материал подчиняется закону Гука. Отсюда следует, что и формула Эйлера справедлива при условии, если:

где предел пропорциональности

Отсюда получаем значение предельной гибкости:

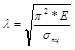
Тогда основной критерий применимости формулы Эйлера получает новый вид:

Для разных материалов значение λ_пр различно.

Если гибкость стержня меньше, то часто пользуются эмпирической формулой Ясинского:

,

где a и b – коэффициенты, определяемые опытным путем, зависят от материала стержня.

Для определения можно пользоваться также формулой в виде:

или

где - предел текучести при сжатии;

- временное сопротивление при сжатии;

- предел пропорциональности при сжатии

Коэффициент запаса устойчивости определяется по формуле

где действующая на стержень нагрузка.

Расчет сжатых стержней на устойчивость

Производится по формуле:

или

, где - площадь поперечного сечения стержня без учета ее ослабления;

- коэффициент уменьшения допускаемого напряжения на простое сжатие

Коэффициент φ зависит от гибкости λ и материала стержня и может быть взят из таблиц.

Условно задачи на устойчивость можно разделить на два типа. К первому относятся задачи, в которых все размеры сечения известны. Ко второму относятся такие задачи, в которых необходимо определить размеры сечения