Другие предметы \ Сопротивление материалов

Расчет прямоугольного сечения в общем случае действия сил. Усилия, вызывающие только нормальные напряжения, страница 3

Критическую силу подсчитывают по формуле Эйлера:

, где

Е- модуль упругости материала;

Imin- минимальный момент инерции сечения (относительно этой оси стержень теряет свою устойчивость);

μl- расчетная или приведенная длина стержня;

μ- коэффициент длины, зависящий от способов закрепления концов стержня. Значение коэффициентов μ для некоторых закреплений стержней приведены на рисунке:

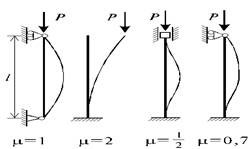
Критическим напряжением называется нормальное напряжение в поперечном сечении центральносжатого стержня, вызванное критической силой:

где λ – гибкость стержня, определяемая по формуле:

imin – минимальный радиус инерции поперечного сечения стержня.

При выводе формулы Эйлера предполагалось, что материал подчиняется закону Гука. Отсюда следует, что и формула Эйлера справедлива при условии, если:

где предел пропорциональности

Отсюда получаем значение предельной гибкости:

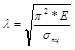
Тогда основной критерий применимости формулы Эйлера получает новый вид:

Для разных материалов значение λпр различно.

Если гибкость стержня меньше, то часто пользуются эмпирической формулой Ясинского:

,

где a и b – коэффициенты, определяемые опытным путем, зависят от материала стержня.

Для определения можно пользоваться также формулой в виде:

или

где - предел текучести при сжатии;

- временное сопротивление при сжатии;

- предел пропорциональности при сжатии

Коэффициент запаса устойчивости определяется по формуле

где действующая на стержень нагрузка.

Расчет сжатых стержней на устойчивость

Производится по формуле:

или

, где - площадь поперечного сечения стержня без учета ее ослабления;

- коэффициент уменьшения допускаемого напряжения на простое сжатие

Коэффициент φ зависит от гибкости λ и материала стержня и может быть взят из таблиц.

Условно задачи на устойчивость можно разделить на два типа. К первому относятся задачи, в которых все размеры сечения известны. Ко второму относятся такие задачи, в которых необходимо определить размеры сечения.

8. Задача Эйлера. Формула Эйлера для критической силы. Зависимость критической силы от условия закрепления концов стержня. Коэффициент приведения длины.

Задача Эйлера: задача о равновесии стержня, сжатого центральными силами Р.

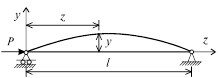
Положим, что по какой-то причине сжатый стержень несколько изогнулся. Рассмотрим условия, при которых возможно равновесие стержня с изогнутой осью.

Координаты точек упругой линии стержня обозначим через z и y. При малых прогибах:

Изгиб стержня происходит в плоскости минимальной жесткости, поэтому под величиной I понимают минимальный момент инерции сечения.

Изгибающий момент М по абсолютной величине равен Ру. Условимся считать положительным тот момент, который увеличивает кривизну. А момент силы Р еще сильнее искривляет упругую линию, т. е. Уменьшает кривизну.

(1)

Обозначим: (2) , тогда уравнение (1) примет вид:

, откуда

Постоянные и должны бать выбраны так, чтобы были удовлетворены граничные условия: при z=0, y=0 и при z=l*y=0. Из первого условия вытекает, что , а из второго

Это уравнение имеет два возможных решения, либо , либо

В первом случае получается, что перемещения обращаются в нуль, и стержень имеет прямолинейную форму.

Во втором случае: , где n – произвольное целое число.

Учитывая выражение (2) получаем:

Скачать файл