Расчет прямоугольного сечения в общем случае действия сил. Усилия, вызывающие только нормальные напряжения, страница 2

Здесь tgβ>0 и β<0. При ,тогда α=-β, т. е. Плоскость действия сил перпендикулярна нейтральной линии и следовательно, косой изгиб невозможен (квадрат, круг). Полный прогиб определяется как геометрическая сумма из прогибов по направлению главных осей OX и OY, тогда

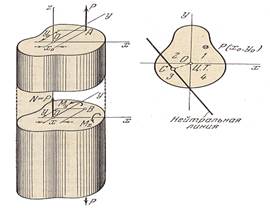
6. Внецентренное растяжение- сжатие. Определение положения нейтральной линии и нормальных напряжений в произвольной точке сечений.

Деформация внецентренного растяжения или сжатия возникает тогда, когда равнодействующая Р всех сил , приложенных к стержню, параллельна оси стержня, но не совпадает с ней. Две равные, но противоположно направленные силы Р, мысленно приложенные в точке О и направленные по оси стержня, не изменяют силового воздействия на стержень, но одна из них вызывает деформацию растяжения или сжатия, а другая в совокупности с равнодействующей образует пару сил, вызывающих косой изгиб. Тогда на основании принципа независимости действия сил напряжение в любой точке определяется по формуле:

Если учесть, что , тогда

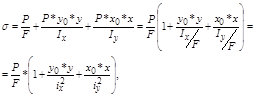
где Р- сила, приложенная в точек С

координаты точки приложения силы

координаты точки, где требуется определить напряжение.

радиусы инерции сечения относительно главных центральных осей сечения

F- площадь сечения.

Направление координатных осей может быть любым. Сила Р берется со знаком «плюс» при растяжении и со знаком «минус» при сжатии.

Координаты берутся со своими знаками, знак у σ получается автоматически.

Допустив, что σ=0, получим уравнение нейтральной линии:

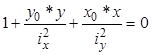
Используя это уравнение, получим величину отрезков, отсекаемых нулевой линией на координатных осях:

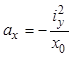(при y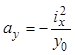=0); ( при x=0)

Свойства нейтральной линии:

- при внецентренном растяжении или сжатии Н. Л. никогда не будет пересекать тот квадрант, где приложена сила;

- если точка С будет приближаться к центру тяжести по прямой , соединяющей эти точки, то Н. Л. будет удаляться от точки О параллельно самой себе;

-положение Н. Л. не зависит от значения и знака силы Р;

-если полюс расположен на одной из главных центральных осей инерции (здесь X или Y), то Н. Л. будет перпендикулярна этой оси;

- Н. Л. делит поперечное сечение на две области: в одной из них в любой точке напряжения растягивающие, в другой- сжимающие. Максимальные напряжения будут в точках, наиболее удаленных от Н. Л. Если Н. Л. не пересекает поперечное сечение, то в любой его точке напряжение будет одного знака. Геометрическое место точек приложения равнодействующей силы в последнем случае называется ядром сечения. Конструктивное обеспечение условий приложения силы в пределах ядра сечения важно для расчета стержней из многих материалов, воспринимающих преимущественно только или растяжение, или сжатие.

7. Понятие об устойчивости. Устойчивое и неустойчивое упругое равновесие. Критическая и допускаемая сила. Коэффициент запаса устойчивости.

Различают устойчивые и неустойчивые формы равновесия упругих систем. Сила Р, которая переводит систему из устойчивого в неустойчивое положения равновесия, называется критической.

Эту силу, для центральносжатых стержней , определяют из условия того, что наряду с прямолинейной формой равновесия стержня возможна, при сколь угодно малых отклонениях, криволинейная форма его равновесия.