Начальная концентрация рассматриваемого элемента в частице. Процесс фазового перехода для сферических частиц

ОБЩИЕ ПОЛОЖЕНИЯ

Рассматривается нестационарная задача тепломассообмена частиц различных материалов на основе решения внутренней задачи с учетом условий влияния внешней среды.

В этом случае процесс нестационарного тепломассообмена описывается уравнением теплопроводности и молекулярной диффузии для частиц сферической формы с граничными условиями 3 рода. Система дифференциальных уравнений, а также граничные условия для безразмерной относительной температуры и концентрации имеют вид [1]:



 ∂C~д = ~r12 ∂∂~r ~r 2 ∂∂C~r~

∂Fo

                ^∂∂ΘД          1 ∂ ~r ₂ ∂∂Θ~r 

=

                    Fo      Lu ~r 2 ∂~r 

                   ^C^~Foд=0 =0 Θ _FoД=₀ =0                      ,                                        (1)



∂~r~r=0

∂∂∂CC~r~~~r=1 ==Bi0 д(1∂∂Θ−~r C~~r=)0 =∂∂0Θ~r~r=1 = Bi(1−Θ)

 где C^~ = C^C_*⁻−^CC⁰₀ - безразмерная относительная концентрация;

С0 - начальная концентрация рассматриваемого элемента в частице, моль/м³;

            С^*     - концентрация этого элемента в окружающей среде, моль/м³;

Θ = ср^{t −}−^t0t0 - безразмерная относительная температура; t₀ - начальная

t

температура частицы, ⁰С;

            tср              - температура окружающей среды, ⁰С;

            R          - радиус частицы, м;

~r = ^r  - безразмерный радиус; R

              Lu     - число Льюиса;

Fo_д  - диффузионное число Фурье;

Bi_д  - диффузионное число Био;

Bi 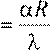 - число Био;

D- коэффициент диффузии, м²/с; β  - коэффициент массоотдачи, м/с;

a - коэффициент температуропроводности частицы, м²/с; λ - коэффициент теплопроводности частицы, Вт/(м⋅К); α - коэффициент теплоотдачи, Вт/(м²⋅К); τ - время, с.

Процесс фазового перехода для сферических частиц диаметром 0,025⋅10^-3÷3⋅10^-3 м, у которых критерий Био изменяется в диапазоне 0,1÷10 описывается соотношением вида [2]:

 Fo − Fo0 = КоBi (δ − δ0 ) + 1n n1+1 + Ko2 (δ2 − δ02 ). (2)

где Fo = ^aτ₂ ; Fo₀ = ^aR^τ₂0 - число Фурье; R

τ₀ - время нагрева частицы до температуры расплавления, с; τ - время нагрева, с;

Ко =Lпл / с⋅(tпов - tпл) - критерий Коссовича; tпов - температура поверхности, ⁰С; tпл - температура плавления, ⁰С;

            Lпл            - скрытая теплота фазового перехода, кДж/кг;

δ =ξ /R ; δ₀ =ξ₀/R ; ξ₀ - толщина расплавленной корочки за время τ₀, м; ξ =ξ(τ)- закон перемещения плоского фронта расплавления; n - показатель параболического закона распределения температуры.

На основе уравнения (2) рассчитывается время расплавления частиц, которое можно учитывать как признак изменения фазового состояния при расчете процесса теплообмена.

Краевая задача решается методом разделения переменных с использованием быстросходящихся рядов. Особенность методики решения заключается в построении схемы расчета, которая позволяет получать результаты, характеризующие связь между определяющими параметрами задачи в заданном любом интервале переменных, представленных как в критериальной, так и в размерной физической формах. Этапы методики расчета.

1.  Построение для среднемассовых безразмерных температуры Θ_мас и концентрации С_мас с использованием аналитических уравнений вида зависимости Θ_мас = Θ_мас(Foд ,Lu, Bi), C_мас = C_мас(Fo_д,Bi_д) для заданного диапазона изменения критериев подобия, соответствующего условиям рассматриваемых систем.