Начальная концентрация рассматриваемого элемента в частице. Процесс фазового перехода для сферических частиц, страница 5

Для добавления линии тренда к имеющейся на диаграмме графической зависимости необходимо выделить линию графика, зайти в меню Диаграмма и выбрать команду Добавить линию тренда. Далее в появившемся диалоговом окне в закладке Тип необходимо определить тип линии тренда (имеется линейная, полиномиальная, логарифмическая, экспоненциальная и степенная), а в закладке Параметры пометить флажком строку показывать уравнение на диаграмме и задать значение прогнозируемых данных.

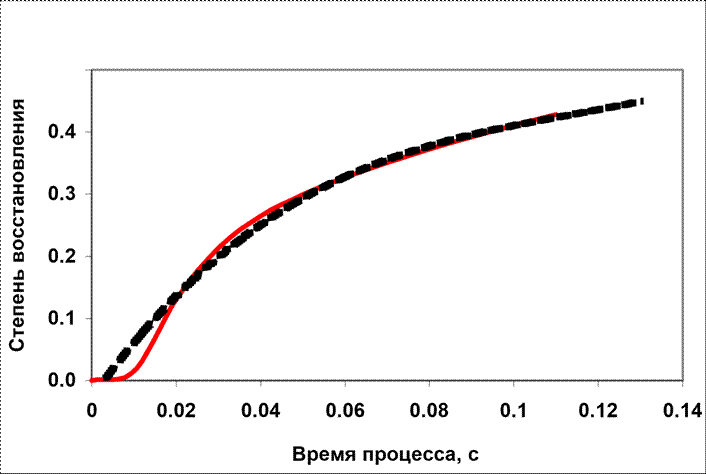
На рис. 8. показан исходная зависимость степень восстановления частицы радиусом 0,5 мм от времени процесса и результат ее аппроксимации полиномом третьего порядка. На рисунке сплошной линией показана исходная зависимость, а пунктиром – линия тренда, которая прогнозирует значение степени восстановления для времени процесса равного 0,13 с.

Определение зависимости степени восстановления

от времени прцесса

                 ^0.5           y = 212.19x ³ - 72.519x ² + 9.5105x - 0.0272

Рис. 8 Результат аппроксимации зависимости степени восстановления частицы от времени процесса

По результатам выполнения исследования должен быть сделан вывод, в котором необходимо объяснить физический смысл полученных коэффициентов аппроксимирующего уравнения.

3. Построение линейных моделей в окрестности заданных значений определяющих факторов на основе полного факторного эксперимента (ПФЭ).

В полном факторном эксперименте реализуются все возможные комбинации факторов на всех выбранных для исследования уровнях. При проведении экспериментов на двух уровнях для трех факторов количество опытов равно N=2³=8, а матрица планирования будет иметь следующий вид.

Таблица 1 Полный факторный эксперимент 2³

На основе данного плана можно построить следующее линейное уравнение регрессии:

^

y = b0 + b1 X1 + b2 X 2 + b3 X 3 + b12 X1 X 2 + b23 X 2 X 3 + b13 X1 X 3 + b123 X1 X 2 X 3

(10)

Коэффициенты этого уравнения в кодированных переменных определяются по следующим соотношениям :

                              ∑N yi                                       ∑N X1i yi                                        ∑N X2i yi                             ∑N X3i yi

                  b0 = i=1N    ,           b1 = i=1 N      ,            b2 = i=1 N       ,           b3 = i=1 N                  ,

∑N X1i X2i X3i yi

                   b123 = i=1                                        ,

N

= ^j − ^{x0j x} где X _{j ∆}x _j , x_j – натуральная переменная, x_j⁰ – опорный уровень, ∆x – интервал варьирования.

Рассчитав коэффициенты уравнения, получим линейную модель, для которой необходимо получить уравнения в натуральных переменных. Затем необходимо определить область изменения управляющих факторов, в переделах которой расхождение этого уравнения с результатами моделирования полученными на основе рассмотренной выше системы уравнений (1)-(3) не будет превышать заданного значения среднеквадратичного отклонения (СКО) параметра ε, который определяется по уравнению:

                   å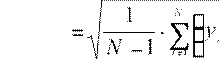.                                                           (11)