Начальная концентрация рассматриваемого элемента в частице. Процесс фазового перехода для сферических частиц, страница 2

2.  Решение обратной задачи при различных Θ_мас и Bi, С_мас и BiД на основе результатов этапа 1 и численное определение характера связи времени массообмена и теплообмена от параметров в критериальной форме FoД = FoД (С_мас, BiД), Fo= Fo(Θ_мас, Bi), где  Fo=Foд /Lu.

3.  Построение номограмм, определяющих количественную связь между конкретными физическими величинами

                                         ττC_t == RaD22 FoдΘCмасмас,α,λβRDR==τtτ(Сα(,β,RR),)                   (3)

R Fo

Гидродинамические условия внешней среды, характеризуются безразмерным критерием Рейнольдса [3]:

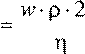                   Re ^R                                                                               (4)

где w - скорость движения внешней среды, м/с; ρ - плотность среды, кг/м³; η - коэффициент динамической вязкости среды, кг/(с м); R - радиус частицы, м.

Интенсивность процессов теплообмена оценивается по безразмерному критерию Нуссельта:

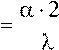                   Nu ^R                                                                                   (5)

В работе [4] приведена экспериментально полученная зависимость, определяющая критерий Нуссельта при Re = 0÷100:

                  Nu = 2 + 0,6Pr ^0,33 ⋅ Re^0,5                                                                                                                             (6)

где Pr  - критерий Прандтля.

Рассчитывая значение критерия Нуссельта по уравнению (6) из соотношения (7) определяется коэффициент теплоотдачи для частицы заданного размера в зависимости от гидродинамических условий внешней среды.

Интенсивность процессов массообмена оценивается по безразмерному критерию Шервуда:

                   Sh ^R                                                                                    (7)

Расчетное значение критерия Шервуда определяется по экспериментально полученной формуле [5]:

                   Sh = 2 + 0,6Sc^0,33 ⋅Re^0,5                                                                                                                                 (8)

где Sc  - критерий Шмидта.

Используя соотношения (7) и (8) находится значение коэффициента массоотдачи.

В тоже время, если имеются частицы или капли очень малого размера d_k ≤ 10^-4 м, то они рассматриваются как твердые сферические частицы, перенос вещества в которых происходит только за счет молекулярной диффузии, то коэффициент массоотдачи по дисперсной фазе β определяется уравнением [6]

π^D ,    (9) β =

3R

Структура рассмотренной модели тепломассообмена без раскрытия процессов фазового перехода представлена на рис. 1. При численной реализации методики изменение параметров системы при фазовом переходе учитывается следующем образом. На каждой итерации сначала по составу определяется температура плавления, затем рассчитывается текущая температура, по которой определяется коэффициент диффузии с учетом фазового состояния частицы. После чего на следующей итерации определяются новые теплофизические параметры материала с учетом полученного состава и фазового состояния.

ОПИСАНИЕ ЛАБОРАТОРНОЙ СИСТЕМЫ

Лабораторная система “Моделирование тепломассообмена в дисперсных системах” создана на кафедре “Информационные технологии в металлургии”, реализована на ЭВМ средствами табличного процессора Excel и позволяет рассчитывать процессы тепломассообмена дисперсных

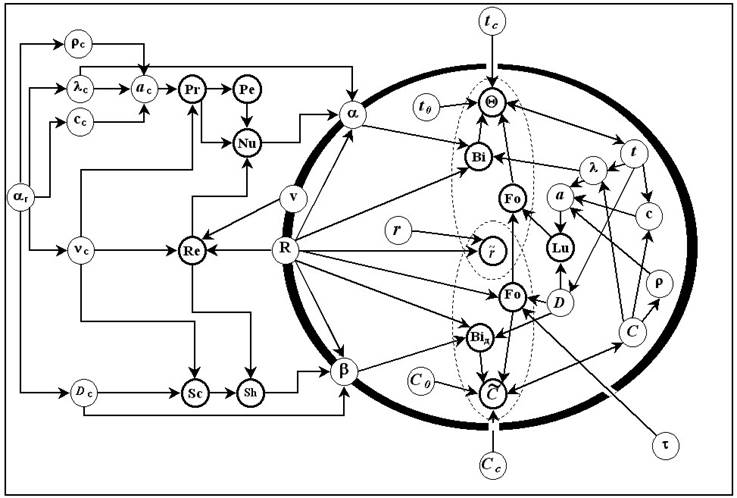
Рис. 1. Структура модели тепломассообмена частиц с учетом фазового перехода. Система предназначена для моделирования и исследования процессов тепломассообмена в различных дисперсных системах.

Функции системы. Основными функциями системы являются следующие.

1. Исследование влияния одного из основных входных факторов системы:

•  продолжительности процесса взаимодействия частиц с внешней средой;

•  температуры внешней среды;

•  размера дисперсных частиц на выходные параметры процесса:

•  время расплавления частицы;

•  среднемассовая температура; • коэффициент диффузии и массоотдачи;

•  степень восстановления.

2. Исследование совместного влияния двух факторов (размер частицы и время процесса) на параметры процесса: