|
Таблица 3.1 - Коэффициенты формулы (3.21)
|
Необходимо отметить, что экспериментально угол сдвига может быть определен по формуле [49]:
(
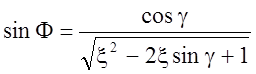3.22)
В случае нестационарного процесса резания, т. е. при переменных толщине среза, углах лезвия, скорости резания и т. д. необходимо учитывать изменение указанных величин во времени и его влияние на угол сдвига. К сожалению, обзор литературы показал на недостаток таких работ.
|
Рисунок 3.16– К определению угла сдвига при переменной толщине среза |
Рядом автором (Кейнт и Гупта [[xiv]], Шоу, Кошияби и др.) отмечается, что в случае переменной толщины среза мгновенная величина угла сдвига описывается формулой:
, (
3.23)
где d - угол наклона поверхности; 
–
коэффициент, который согласно различных исследований [70] может принимать значения от 0.2 до 1 в зависимости от угла сдвига 
.
Также одной из важных характеристик процесса стружкообразования
является удельная работа пластической деформации 
(работа
отнесенная к единице объема деформируемого материала). Общепринято [11, 43], что
. (23)
А. М. Розенбергом сделал вывод,
что не влияет температурно-скоростной фактор.
Многими учеными широко применяется (Мерчант [35], Е. М. Трент [56] со ссылкой на Дж. В. Роува и П. Т. Спика, В. С. Кушнер [[xv], стр. 28] и др. ), принцип минимума энергии для определения указанных характеристик. Причем рассматривают как только минимум энергии деформации (Мерчант) так и минимум полной энергии для определения характеристик стружкообразования (В. С. Кушнер, Е. М. Трент).
Хотелось бы отметить принцип нестабильности
равномерного распределения адиабатической пластичности, который был
предложен Помеем [58]. При адиабатических условиях в первоначально гомогенной и
анизотропной среде при однородной температуре создается равномерное течение
материала в одном направлении в плоскопараллельных поверхностях таким образом,
что деформация возрастает непрерывно и достигает момента, когда течение
приобретает критическое значение 
, такое , что
новому 
соответствует понижение 
сопротивления сдвигу. Это, при случайно
возникшем возмущении, приводит к локализации работы деформации, что повышает
температуру в тонком слое легкого течения материала, в то время как в остальной
части твердого тела температура стабилизируется и может возникнуть даже упругое
состояние. Этот принцип в основном применяют для объяснения контактных
процессов, хотя Шоу [57] указывает на возможность существования подобного явления
в УПС[I1] .
[i] Shaw M. C. The theory of metal cutting. // Proceedings of the twenty-fifth international machine tool design and research conference, Birminhem, –1985. – P. 33-36.
[ii] Pomey J. Phenomens de mecanique ohysique qui regissent la coupe des metaux // Mecanique materiaux electricite. 1971 pp. 8-35
[iii] Тихман С. И. Расчетная схема стружкообразования с учетом сжатия в очаге деформации//Развитие процессов резанияи холодного пластического деформирования металлов. –К.: ИСМ им. В. Н. Бакуля, 1994. –С.25-30
[iv] Мазур М. П. Термомеханична теорія розрахунку параметрів контактної зоні при різанні пластичних матеріалів// Проблеми сучасного машинобудування/Збірник наукових праць. –Хмельницький: ТУП, 1996. –С. 8-12.
[v] Кушнер В. С. Термомеханическая теория процесса непрерывного резания пластических материалов. –Иркутск: Изд-во иркутского ун-та, 1982. –180с.
[vi] Танака Ё. Исследование высокоскоростного резания// «Сэймицу кикай». –1969. Т. 35. №7. –С. 458-463
[vii] Shaw M. C. A New Mechanism of Plastic Flow.// Int. J. of Mech. Science. – 1980. –Vol. 22, p. 673
[viii] Розенберг О. А., Огородников В. А. Прогнозирование ресурса пластичности и управление технологической наследственностью в процессах холодного пластического деформирования с помощью феноменологической теории деформируемости без разрушения//Высокие технологиии в машиностроении. –Х.: ХДПУ, 1998. С. 249-251
[ix] Кабалдин Ю. Г., Шпилев А. М., Просолович А. А. Синергетический анализ причин возмущения вибраций при резании//Вестник машиностроения. –1997. №10. С. 21-29
[x] Резников А. Н. Теплообмен при резании и охлаждении инструментов. –М.: Машиностроение, 1963. –200с.
[xi] Виноградов А. А. О теоретическом угле сдвига при резании пластичных материалов. Докл. VI Краковской конф. «Достижения теории технической обработки материалов», 1990
[xii] Мироненко С. В. и др. Определение закономерностей адгезионного взаимодействия режущего инструмента с обрабатываемым материалом. –Одесса: ОГПУ, 1994. –7с. ДЕП в ГНТБ Украины в 1994 №2064-УК94
[xiii] Силин С. С. Козлов В. А. К вопросу теоретического расчета сил резания// Производительная обработка и технологическая надежность деталей машин. –Ярославль, 1977. Вып. 6. –С. 3-6
[xiv] Kainth G. S., Gupta R. G. Shear angle relationship with variable undeformed chip thickness// ASME conference 11th -15th of November 1973, Detroit, Michigan, USA
[xv] Кушнер В. С. Решение задач механики и теплофизики с применением теории эксперимента и АВМ. –Омск: ОПИ, 1976. – 80с.
Стр: 1
[I1]Написать о методах
расчета сил резания
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.
и 
постоянны и не зависят от b. Не подтверждается экспериментом. 
. Выдвинуто предположение, что
УПС не является плоскостью максимальных касательных напряжений. 
. 
). Формула
получена из условия равновесия инструмента. 
