Современные представления о деформационных процессах, страница 2

В тоже время В. С. Кушнер показал, что деформация в зоне А осуществляется по схеме неоднородного сдвига в направлении границ этой зоны [52, стр. 9]. Зона А может включать либо дну широкую область деформаций (область упрочнения обрабатываемого материала), либо широкую область упрочнения материала и узкую область локализованных у конечной границы деформаций, в которой материал существенно не упрочняется.

Мерой деформаций является относительный сдвиг e [11 и др.]. При резании и он может составлять сотни процентов [43].

Еще одной из характеристик деформации может служить угол текстуры  (рисунок 3.11), представляющий собой угол наклона большей оси эллипса к условной плоскости сдвига [11]. Этот показатель связан прямой функциональной связью с e. Его широко использовал В. С. Кушнер при анализе зон А, Б, В, Г [52, стр. 10].

Кроме того в теории пластичности деформации принято характеризовать интенсивностью деформаций  (для простого сдвига) [11].

В работе [11] отмечается, что А. М. Розенберг предложил определять деформированное состояние углом  или параметром . Этот параметр позволяет определить долю деформаций сдвига во всей деформации.

Для определения степени деформации часто применяется формула [11; 43 и др.]:

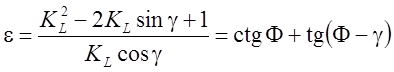.                                   ( 3.2)

Из этого уравнения следует, что при  степень деформации . Хотя хорошо видна однозначная функциональная зависимость .

Предложенная И. А. Тиме модель стружкообразования с одной плоскостью сдвига предполагает наличие скачкообразного изменения скорости частиц удаляемого материала с  на , что невозможно из условия неразрывности [11]. Поэтому принимается, что витки сбегающей стружки (рисунок 3.12, а) являются параллельными, прямыми при возрастании и убывании области пластичности. В тоже время в узкой области пластичности витки изгибаются и сопрягаются касательно с прямыми возрастания и убывания. Характерный годограф скоростей Прагнера, определяющий скорости смещений частиц вдоль УПС приведен на рисунке 3.13. Скорость в какой-либо точке витка , образует угол  с  [58, 35]. Исследования Помея показали, что линии течения могут быть представлены короткой дугой параболы (рисунок 3.12,б), соприкасающейся с прямыми линиями по обеим сторонам возрастания и убывания [58].

Необходимо различать скорость сдвига  (рисунке 3.7,б) т. е. скорость, с которой осуществляется сдвиг по УПС, и скорость деформации , определяемы по формулам [11, 58 и др.]:

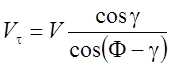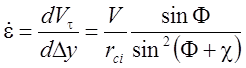;  ,                   ( 3.3)

где  - радиус кривизны линий течения [58]. Часто делается предположение, что скорость деформации является постоянной в УПС.

Выделяют три области скоростей деформации: с^-1 – при механических испытаниях;  с^-1 – при резании на микроскоростях;  с­^-1 – при высоких, обычно применяемых на практике скоростях [стр. 22, 43].

При этом Ю. Г. Кабалдин указывает на то, что в зонах стружкообразования и вторичной деформации относительная деформация e и скорость деформации  могут достигать критических значений (ед. и с^-1) [65].

Очевидно, что деформации приводят к возникновению напряженного состояния в УПС. В настоящее время нет единого мнения о законе распределения касательных и нормальных напряжений в условной плоскости сдвига. За условие начала образования стружки принимают, что максимальные касательные напряжения в УПС достигают определенного предела t_р. Эту величину С. С. Силин и др.  называют сопротивлением пластическому сдвигу [51]. По существу она может быть эквивалентна (в зависимости от подхода и свойств обрабатываемого материала) пределу текучести [11] или пределу прочности [58] на сдвиг в данных условиях деформирования.  

По мнению В. Ф. Боброва [11] (со ссылкой на Н. Н. Зорева [54] ) и Трента  Т. Н. [56]  не зависит от степени деформации и температурно-скоростного фактора, являясь тем самым постоянной механической характеристикой, соответствующую пределу текучести при простом растяжении-сжатии. (По сути это Н. Н. Зорев выдвинул указанную гипотезу и она нашла широкое применение и признание). Н. Н. Зорев [54] предложил гипотезу о равенстве касательных напряжений при резании и сжатии в условиях равенства относительных сдвигов (единую кривую течения). На основании этой гипотезы и собственных экспериментов С. С. Силин определяет  по формуле [51]

,                                                                   (3.4)

где  - коэффициент группы обрабатываемого материала.

Большинство этих авторов влияние скорости деформаций и температуры непосредственно на напряжения не рассматривали (В. Ф. Бобров, Н. Н. Зорев), либо считали (Ш. Кобаяши, Э. Томсен [стр. 11, 43]), что это влияние противоположно и взаимно компенсируется.

Как указывает С. С. Силин [51, стр. 71]  Т. Н. Лоладзе предложит принимать

.                                                            (3.5)

Он отметил значительное разупрочняющее влияние температуры на сопротивление сдвигу при резании предварительно нагретого и охлажденного до низких температур материала (опыты И. Финни и И. Улэка) [52]. В своих ранних работах В. С. Кушнер [71] предложил формулу

.                                                         ( 3.6)

На основании экспериментальных исследований Г. Л. Куфарев и др. [стр. 11, 43; 55] приходят к выводу, что при резании с микроскоростями существует единая кривая течения. При высоких скоростях единой кривой течения нет, что авторы объясняют взаимным влиянием скорости деформации и температуры в зоне сдвига.

Исследования А. М. Розенберга и других ученых [43] опровергают существование единой кривой течения. Они выдвинул гипотезу о равенстве работ пластической деформации в процессах резания и сжатия при равных относительных сдвигах в этих процессах. Они показали на наличие зависимости  (упрочнения). Ими была предложена формула:

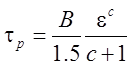,                                                    ( 3.7)

где В и с – константы материала, определяемые из опытов на сжатие. А. М. Розенберг [43, стр. 15] со ссылкой на эксперименты П. Бриджмена показал, что при глубоком сжатии и резании сталей предельного упрочнения и тем более разупрочнения не наблюдается. Этот эффект был отмечен при сжатии меди. Однако объяснения физической природы такого явления не приведено. А. М. Розенберг также отвергает влияние температурного фактора на напряжения в УПС. В доказательство он приводит экспериментальное подтверждение и объяснение этому явлению [43]: