Современные представления о деформационных процессах, страница 3

на кривую удельной работы деформации укладываются результаты опытов как с высокими скоростями резания (в условиях интенсивного нагрева) так и с микроскоростями, где нагрев не происходит;

нет разницы в твердостях стружек, снятых при этих скоростях резания при одной и той же степени деформации.

Причинами этого он считает [43]: 1) кратковременность процесса деформации в зоне сдвига (~10­^-4 с) и процессы разупрочнения (под влиянием нагрева) не успевают протекать (с) точно также как и структурные превращения (~0.1 с); 2) выделяемая теплота не предшествует деформации, а следует за ней, так как является ее результатом. 

Отмечается также [43], что скорость деформации влияет на напряжения в УПС при резании только легкоплавких материалов (свинца, алюминия) и не влияет на резание тугоплавких металлов. Они объясняют этот эффект  наличием т. н. предельного скоростного упрочнения сталей (уменьшение влияния скорости деформации с увеличением ее величины).

Исследования В. С. Кушнера [52], Оксли [35], Шоу [57], Помея [58], указывают на еще более сложную зависимость сопротивления сдвигу.

В. С. Кушнер допускает существование единой кривой течения  при резании и пытается учесть влияние температурно-скоростного фактора на сопротивление сдвигу. Применив соотношение М. А. Зайкова он получил зависимости для расчета предела текучести УПС [52]. В основе этих зависимостей лежит положение об адиабатичности процесса деформирования [52]. По его мнению результаты расчета по этим формулам хорошо согласуются с опытами Н. Н. Зорева. Н. П. Мазур [[iv]] ссылаясь на работы В. С. Кушнера [[v]] указывает на то, что сопротивление пластическому сдвигу в процессе непрерывного резания пластичных материалов определяется температурой этой зоны  и истинным пределом прочности на разрыв :

,                                     ( 3.8)

где , 1/С°.

Н. Г. Абуладзе [12] предложил формулу для определения напряжений сдвига:

,                                              ( 3.9)

где  - относительное удлинение при растяжении.

Более того, в теории пластичности известно соотношение между напряжением сдвига и твердостью по Виккерсу [12]:

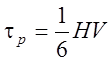,                                             ( 3.10)

или [43]

                                         ( 3.11)

Теоретические и экспериментальные исследования Ё. Танака и др. [[vi]] показали возрастание сопротивления сдвигу с увеличением скорости. Авторы объясняют это  увеличением градиента температуры перед УПС при высоких скоростях, что приводит к  началу сдвига в более охлажденной ненадрезанной зоне. Ими вводится понятие «адиабатическое скольжение» т. е.  катастро­фические деформации, обусло­вленные значи­те­льным градиентом температур при высокой скорости деформации (рисунок 3.14).

В своих исследованиях Оксли [35], Шоу [57], Помей [58] показали (со ссылкой на работы П. Бриджмена), что сопротивление пластическому сдвигу  существенно зависит не только от собственно деформации, скорости деформации и температуры, но и от гидростатического давления (т. н. деформационное упрочнение под действием гидростатического сжатия), что может быть выражено формулой [58]:

,                                                     ( 3.12)

где  - константа материала (для углеродистой стали (после эвтектоидного отпуска) ). Влияние собственно упрочнения при адиабатических условиях и больших деформациях Помей предлагает описывать формулой [58]:

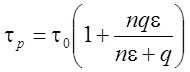,                                                      ( 3.13)

где  - константа материала (зависит от содержания углерода);   - учитывает гидростатическое давление (от атмосферного до высокого гидростатического давления) на УПС. Это выражение корректно при  и учитывает предельное деформационное упрочнение и разупрочнение обрабатываемого материала (ссылка на опыты Чанга, Хегинботана (Chang, Heginbothan) и Бриджмена). Наличие этих эффектов Шоу [[vii]] объясняет явлением образования «внутренних шеек», подобно образованию шейки при простом растяжении-сжатии. По мнению Помея [58] с увеличением скорости деформации увеличивается предел упругости, но на максимальное напряжение () мало влияет, вследствие того, что нагрев и скорость деформации оказывают взаимно противоположное влияние. Необходимо отметить, что рассматривается снижение твердости металла при повышении температуры, а не вследствие влияния рекристаллизации, которая не успевает произойти за короткое время деформаций. Отмечается также наличие явления синехрупкости [58], заключающееся в смещении максимума предела прочности в сторону более высоких температур с увеличением скорости деформаций, что обусловлено блокированием дислокаций в междоузлиях и возрастающей с температурой подвижностью атомов. Описанное выше представление о сопротивлении сдвигу они предложили описать формулой [58]:

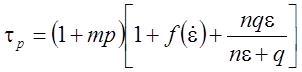,                                      ( 3.14)

где  - коэффициент характеризующий скоростное упрочнение материала. Необходимо отметить, что поскольку он определяется при больших скоростях деформаций то он учитывает и указанные температурные эффекты.

Объяснения представленных зависимостей, как правило, дают с позиции теории дислокаций и термодинамики необратимых процессов. Широко эти вопросы рассматривались Ю. Г. Кабалдиным [65], Друкером, Котреллом [35, стр. 57] и др. В частности, согласно теории Котрелла сопротивление сдвигу при резании будет больше, чем при статическом нагружении, но выше  определенной скорости – оно не будет зависеть от скорости деформации и температуры.

В. А. Огородников и О. А. Розенберг [[viii]]  указывают на то, что в случае монотонного, но сложного деформирования пластичность зависит не только от уровня достигнутых деформаций и схемы напряженного состояния, но и истории деформирования в т. ч. на предыдущих операциях. Ими разработан критерий, учитывающий нелинейный характер накопления повреждений.