Современные представления о деформационных процессах, страница 4

Часто многие авторы принимают (Б. Ф. Бобров, Мерчант, А. М. Розенберг, С. С. Силин, Г. Л. Куфарев и др.), что независимо от рода и свойств обрабатываемого материала, величины переднего угла лезвия, толщины срезаемого слоя и скорости резания, касательные напряжения вдоль УПС имеют постоянную величину. Нормальные  напряжений распределяются по-иному. При больших передних углах инструмента g и малых коэффициентах трения на  нормальные напряжения уменьшаются по мере приближения к лезвию и в некоторой точке УПС могут изменять свой знак на обратный (рисунок 3.15,а). По мере уменьшения переднего угла инструмента g и увеличения коэффициента трения  указанная эпюра постепенно переходит к виду эпюры, изображенной на рисунке 3.15,б, на которой нормальные напряжения s сохраняя постоянство знака, увеличиваются при приближении к лезвию. Отмечается, что нормальные напряжения s в УПС не постоянны и отсутствует их влияние на величину касательных напряжений. При этом величину касательных напряжений можно определять либо по формуле [11]:

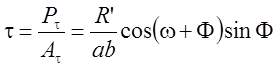                                ( 3.15)

либо по формуле [43]:

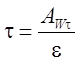 .                                                           ( 3.16)

И. Дж. А. Армарего указывает [35], что вычисленные по первой из этих формул напряжения оказываются несколько завышенным по сравнению с величиной сопротивления сдвига. Отмечается, что объяснением этому могут служить внешние эффекты. Это, во-первых, эффект трения на задней поверхности. Сила трения на задней поверхности входит составной частью в изменяемую силу резания, но не влияет на процесс сдвига. Во-вторых, во многих случаях резания существует так называемая зона опережающего течения, которая увеличивает длину плоскости сдвига, хотя это и не учитывается при аналитическом исследовании.

Ю. Г. Кабалдин [[ix]] с позиции разработанного им механизма образования сливной стружки (основан на теории дислокаций и синергетическом подходе) отмечает, что всякому разрушению среза предшествует порообразование. Разрыхление металла может достигать  0.1-1% в зависимости от степени деформации e. Поэтому следует отдельно выделить истинные касательные напряжения t_и.

Известно, что угол действия равен и, следовательно, зависит от коэффициента трения . Однако С. С. Силин выдвигает гипотезу [51] о том, что  по аналогии с известным положением в сопротивлении материалов.

Исследования Оксли [35], Шоу [57], Помея [58] и др. показали, что касательные напряжения распределены неравномерно по УПС и, как уже отмечалось, зависят от нормальных напряжений s (гидростатического давления ). Экспериментальным подтверждение этому являются работы П. Бриджмена и исследования Шоу методом КЭ. Они предложили (на основании анализа напряженного состояния в УПС с помощью кругов Мора) соотношения между максимальным касательным напряжением t и гидростатическим давлением в любой точке УПС [35, 58] и определение компонент сил резания через них. Полученное распределение сильно похоже на распределение контактных напряжений на передней поверхности (рисунок 3.15,б). Видно, что на некотором расстоянии от вершины режущего клина касательные напряжения могут быль даже меньше предела текучести, что свидетельствует о преобладающем влиянии процесса разрушения  над процессом  текучести материала. Нормальные напряжения монотонно убывают с увеличением расстояния от вершины режущего клина.

Представляет интерес определение угла  и координат точки приложения силы . Оксли предложил простую формулу для определения [35]:

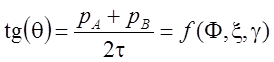.                                                    ( 3.17)

Помей уточнил ее и, приняв ряд гипотез [58], получил довольно сложное выражение для определения угла , которое в упрощенном виде можно записать:

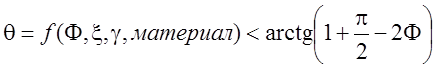.                             ( 3.18)

Кроме этого упомянутыми авторами получены соотношения для определения координат приложения силы  . Например [35]:

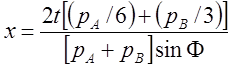;                       ( 3.19)

Необходимо отметить, что широкое распространение получила гипотеза об адиабатичности процесса стружкообразования [51, 52, 58]. Это, прежде всего, оправдано высокими скоростями деформации [52; 43], а также наличием соседних нагретых зон  [52]. Однако реальная картина значительно сложнее из-за наличия стоков теплоты и действительная температура будет несколько меньше [11, 32, 43]. А. М. Розенберг [43] со ссылкой на А. Н. Резникова [[x]] показал это на примере резания стали  ШХ15 со скоростью м/с: при адиабатическом процессе температура в зоне сдвига была бы 480°С в то время как температура при наличии стока теплоты равна 340°С.

Особый интерес представляет определение угла сдвига . Многие авторы принимают его в качестве основного параметра, характеризующего процесс стружкообразования и являющегося мерой пластических деформаций [4, 11, 35, 51 и др.]. Е. Исуи (Isui) отмечает, что соотношение для определения угла сдвига  в общем случае квазистационарного процесса резания может иметь следующий вид:

.                                        ( 3.20)

Предложено огромное множество различных подходов к определению этой функциональной зависимости. По мнению И. Дж. А. Армарего [стр. 50, 35] некоторые полученные формулы могут быть описаны общим выражением:

.                                                         ( 3.21)

В таблице 1 приведена краткая характеристика постоянных  и . Необходимо отметить, что такой подход  из всех условий обработки учитывает только передний угол и коэффициент трения. Угол сдвига  считается независимым от упрочнения, тепловых процессов, анизотропии и др. явлений, хотя в некоторых случаях эти формулы являются обобщением расчетов, учитывающие указанные особенности.

Помимо указанных соотношений известно много других [[xi]]. Все они, как правило, носят более сложный характер и получены совместным решением известных уравнений, связывающих угол сдвига, усадку стружки, и температуру резания . Среди них уравнения В. С. Кушнера  [71, стр. 37;61, стр. 15], С. С. Силин [51, стр. 12], Мироненко С. В. [[xii]].

К интересным выводам пришел С. И. Филоненко [44, стр. 55]. Он считает, что угол сдвига может быть определен как функция только технологических параметров процесса обработки. Однако он не приводит никаких экспериментальных доказательств справедливости своих выводов.