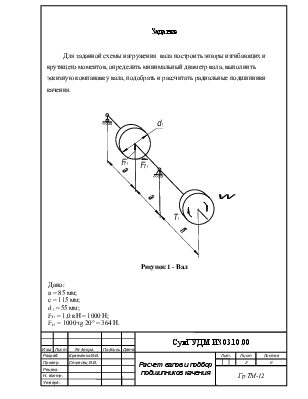
Для заданной схемы нагружения вала построить эпюры изгибающих и крутящего моментов, определить минимальный диаметр вала, выполнить эскизную компановку вала, подобрать и рассчитать радиальные подшипники качения.
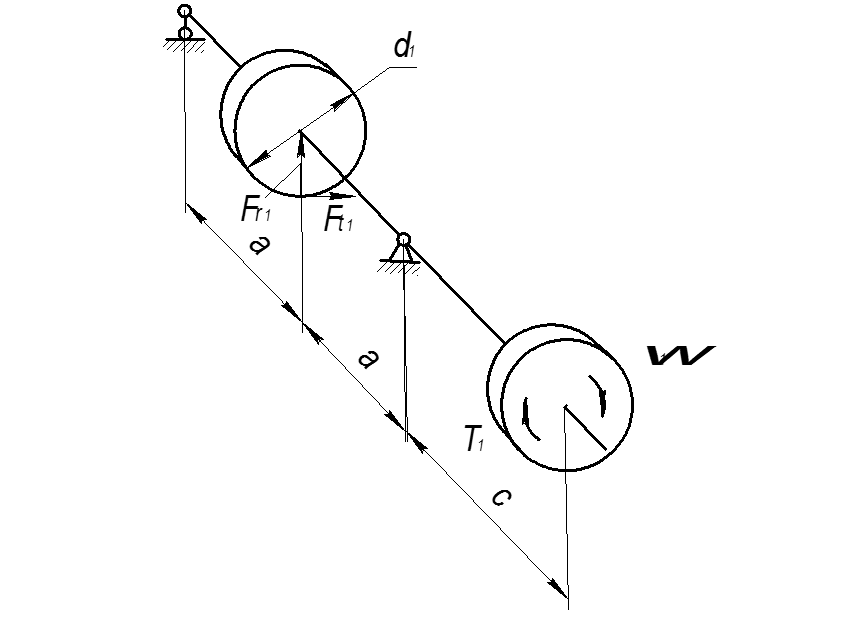
Рисунок 1 - Вал
Дано:
а = 85 мм;
с = 115 мм;
d1 = 55 мм;
Ft1 = 1,0 кН = 1000 Н;
Fr1 = 1000·tg 20° = 364 Н.
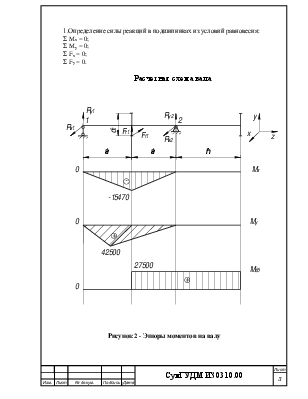
1.Определение силы реакций в подшипниках из условий равновесия:
Σ Mx = 0;
Σ My = 0;
Σ Fx = 0;
Σ Fy = 0.
Рисунок 2 - Эпюры моментов на валу
Для подшипника 1: Σ Мx1 = 0;
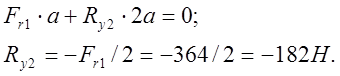
Для подшипника 2: Σ Mx2 = 0;
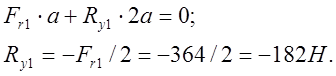
Проверяем условие равновесия Σ Fy = 0:
-182 + 364 – 182 = 0 – условие выполняется.
Для подшипника 1: Σ My1 = 0;
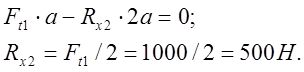
Для подшипника 2: Σ My2 = 0;
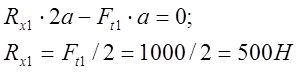
Проверяем условие равновесия Σ Fx = 0:
500 - 1000 + 500 = 0
2.Строим эпюры
a) Σ Mxk = 0;
при z = 0: Mx = 0; при z = a: Mx = -Ry1· a = -182 · 85 =-15470 H·мм.
б) Σ Myk = 0;
при z = 0: My = 0; при z = а: My = Rx1· a = 500 · 85 = 42500 H·мм.
в) Σ Mzk = 0;
Mкр = Ft1 · d1/2 = 1000 · 55/2 = 27500 Н·мм.
3.Определяем суммарные реакции в подшипниках:
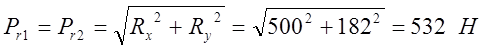
4.Определяем минимальный диаметр вала из расчета на чистое кручение по пониженному допускаемому напряжению без учета влияния изгиба:
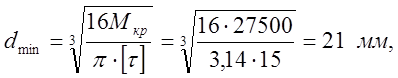
где 
= 15 МПа – допускаемое
напряжение кручения.
Принимаем dmin = 21 мм ( см. Чернавский с.162 ).
Выполняем эскизную компановку вала.
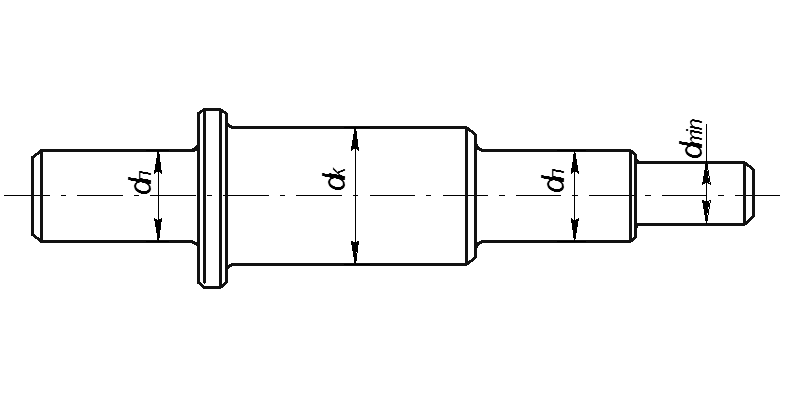
Рисунок 3 - Эскизная компановка вала
Проверяем грузоподъемность подшипников по опоре 1.
Определяем эквивалентную нагрузку:
где 
=
1 – коэффициент условий работы;
= 1 – температурный коэффициент;
V = 1 – коэффициент, связанный с вращением внутреннего кольца подшипника.
Определим
отношение осевой силы к статической грузоподъёмности подшипника: Fa /Со = 0 / 6950 = 0 
е
= 0,19 X = 1; Y =
0.
Рэ = 1· 532 = 532 Н.
6.Определяем номинальную долговечность подшипника:
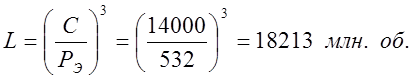
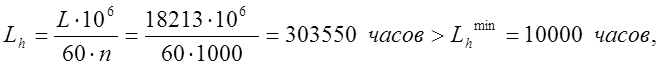
где n – частота вращения подшипника, n = 1000 об/мин.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.