Проверка долговечности подшипника

7. Проверка долговечности подшипника

Вал №2:

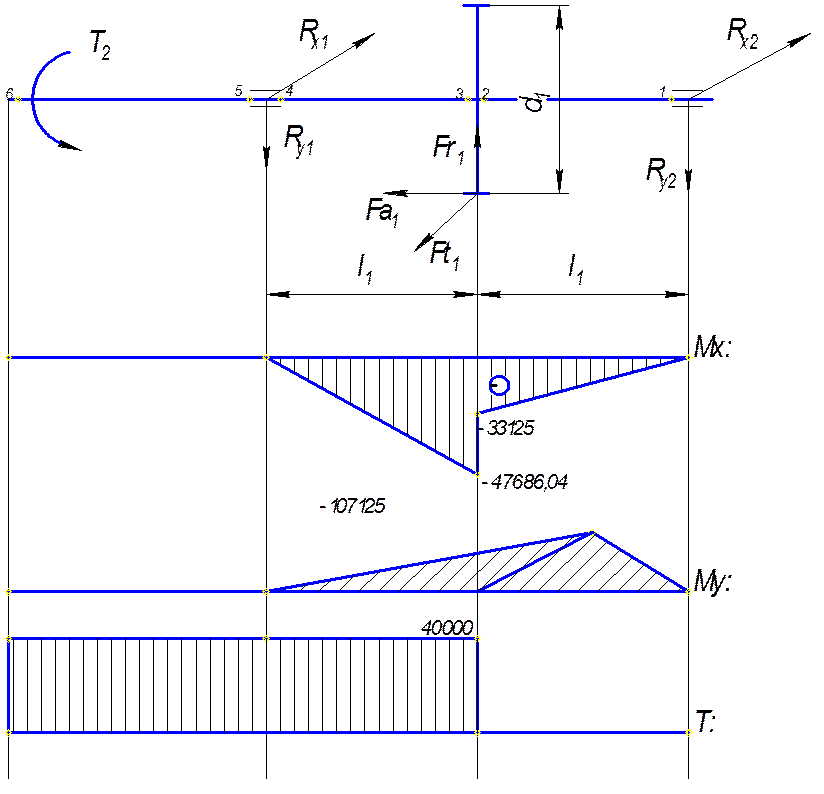
Рисунок 2: Схема нагружения ведущего вала и эпюры изгибающих и крутящего момента

Где: l₁ = 125мм; Fr₁ = 647Н; Fa₁ = 624Н; Ft₁ = 1714Н, d = 64мм.

Определяем силы реакции в подшипниках из условия равновесия:

;

;

;

;

Для подшипника 1 сумма моментов всех сил относительно оси х:

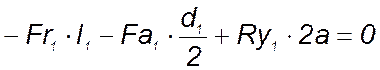                            (131)

Из уравнения (131) следует:

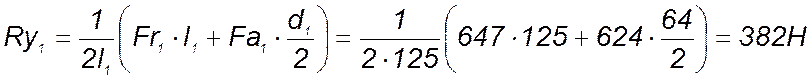  (131)

Для подшипника 2 сумма моментов всех сил относительно оси х: .

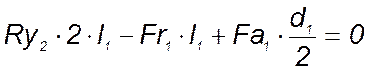                             (132)

Из уравнения (132) следует:

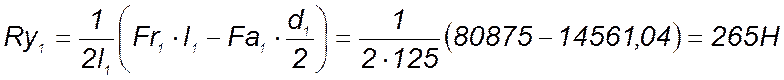  (133)

Проверяем условие равновесия:

                                      (134)

Условие выполняется.

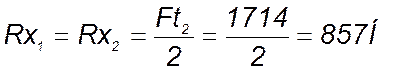                          (135)

Проверяем условие равновесия:

                                       (136)

Условие равновесия выполняется.

Построение эпюр изгибающих и крутящего момента.

Эпюры моментов строим на сжатых волокнах.

Строим эпюру изгибающих моментов относительно оси х (методом контурных точек).

Мх:

Мх₁=0;

Мх₂=

Мх₃=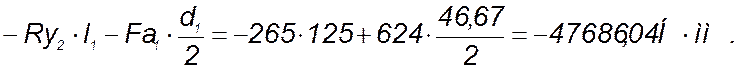

Мх₄=Мх₅=Мх₆=0.

Строим эпюру изгибающих моментов относительно оси у (методом контурных точек).

Му:

Му₁=0.

Му₂=Му₃=

Му₄=Му₅=Му₆=0.

Определяем суммарные реакции в подшипниках.

                    (137)

                    (138)

Выбираем подшипники радиальные шариковые однорядные

[1,с. 392]: 207.

Проверяем грузоподъемность и долговечность подшипника по наиболее нагруженной опоре №1.

Определяем эквивалентную нагрузку действующую на подшипники.

 

где: Кσ =1, - коэффициент, условий работы подшипников;

        Кτ =1, - коэффициент, учитывающий температуру;

V = 1, - Коэффициент, связанный с вращением внутреннего кольца подшипника.

Fa = Fa₁ = 624H.

Определяем отношения:

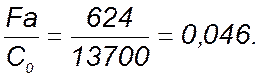
где: С₀ = 13700 Н – статическая грузоподъемность подшипника 207 [1, приложение3].

Тогда по [1, табл. 9.18] определяем е=0,26 – коэффициент осевого нагружения.

Определяем отношение Fa к Pr₂ (на наиболее нагруженный подшипник):

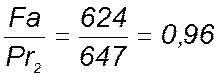
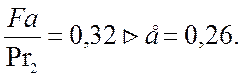
Следовательно выбираем коэффициенты x и у по [1, табл. 9.18]: х = 0,56; у = 1,71.

Определяем долговечность подшипников в 1000000 оборотов.

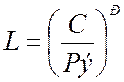                                            (139)

где: С=25500 Н [1, приложение 3].

 Р=3 – показатель степени для шариков подшипников.

 

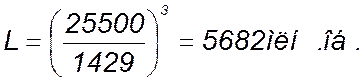
Определяем долговечность подшипника в часах:

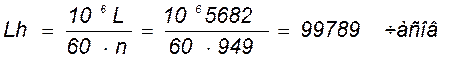                           (140)

где n – частота вращения вала.

.

Долговечность и работоспособность подшипников обеспечена.

Вал № 3:

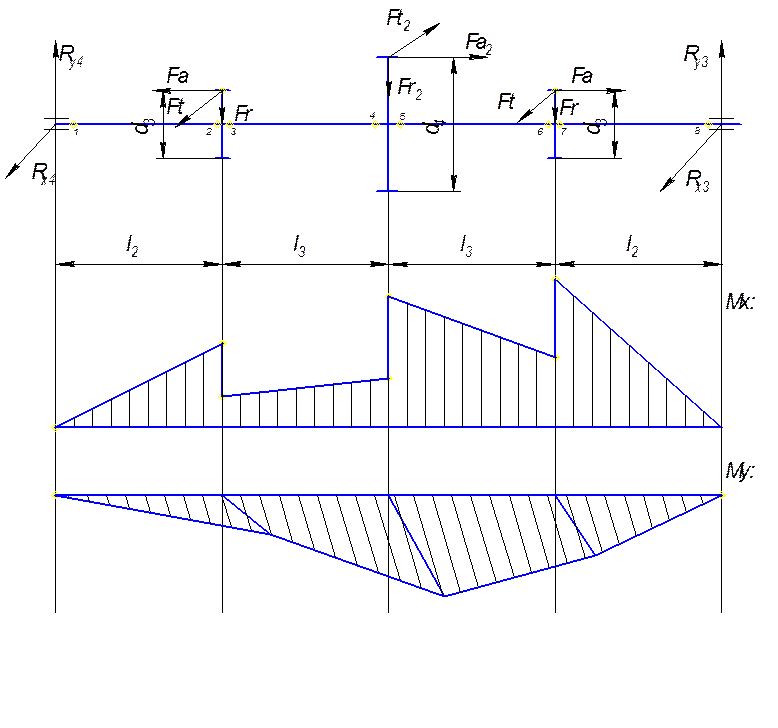
Рисунок 2: Схема нагружения ведомого вала и эпюры изгибающих и крутящего момента

Где d₃ = 64мм; d₄ = 233,33; Ft = 5781Н; l₂ = 53мм; l₃ = 73мм; Ft₂=1714Н; Fr = 2375Н; Fr₂ = 647Н; Fa = 1513Н; Fa₂ = 624Н.

Определяем силы реакции в подшипниках из условия равновесия:

;

;

;

;

Для подшипника 1 сумма моментов всех сил относительно оси х:

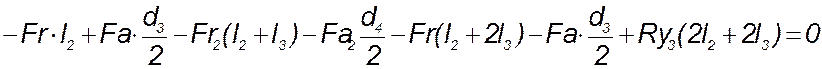 (141)

Из уравнения (141) следует:

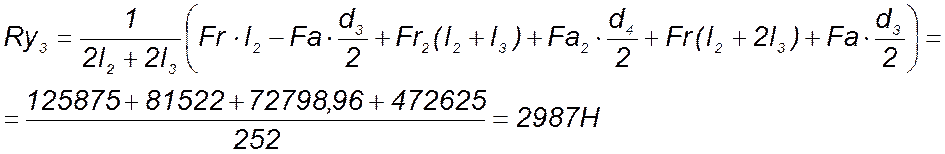
Для подшипника 2 сумма моментов всех сил относительно оси х: .

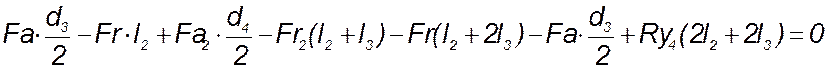  (142)

Из уравнения (142) следует:

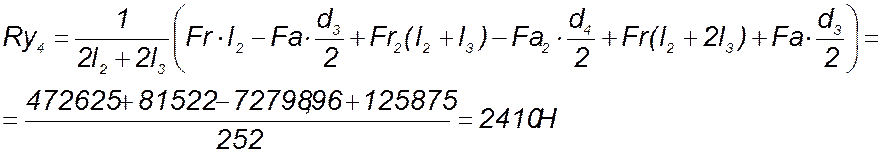
Проверяем условие равновесия:

                            (143)

Условие выполняется.

Для подшипника 1 сумма всех моментов относительно оси у:

        (144)

Из уравнения (144) следует:

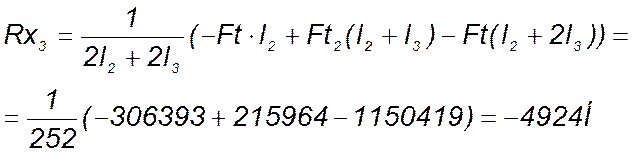          (145)

Для подшипника 2 сумма всех моментов относительно оси у:

        (146)

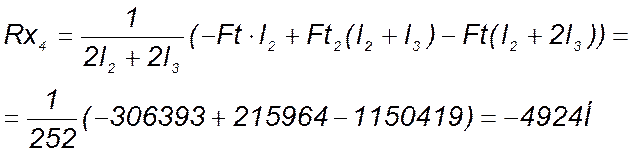         (147)

Проверяем условие равновесия:

                               (148)

Условие равновесия выполняется.

1.  Построение эпюр изгибающих и крутящего момента.

Эпюры моментов строим на сжатых волокнах.

Строим эпюру изгибающих моментов относительно оси х (методом контурных точек).

Мх:

Мх₁=0;

Мх₂=

Мх₃=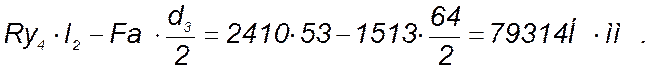

Мх₄=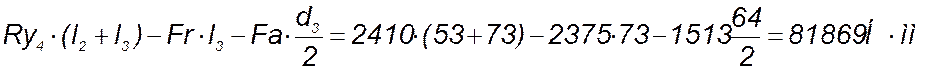                 Мх₅=Mx₄ +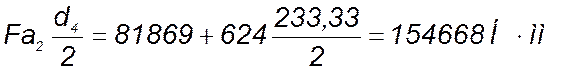

Мх₆=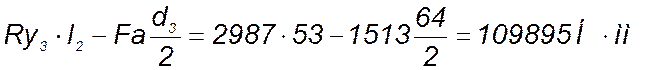

Мх₇=

Мх₈=0.

Строим эпюру изгибающих моментов относительно оси у (методом контурных точек).

Му:

Му₁=0.

Му₂= Му₃=

Му₄= Му₅=

Му₆= Му₇=

Му₈ = 0.

2.  Определяем суммарные реакции в подшипниках.

                    (149)

                    (150)

3.  Выбираем подшипники радиальные шариковые однорядные

[1,с. 392]: 108.

Проверяем грузоподъемность и долговечность подшипника по наиболее нагруженной опоре №1.

Определяем эквивалентную нагрузку действующую на подшипники.

                               (151)

где: Кσ =1, - коэффициент, условий работы подшипников;

        Кτ =1, - коэффициент, учитывающий температуру;

V = 1, - Коэффициент, связанный с вращением внутреннего кольца подшипника.

Fa = Fa₂ = 624H.

Определяем отношения:

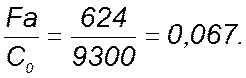
где: С₀ = 9300 Н – статическая грузоподъемность подшипника 108 [1, приложение3].

Тогда по [1, табл. 9.18] определяем е=0,26 – коэффициент осевого нагружения.

Определяем отношение Fa к Pr (на наиболее нагруженный подшипник):

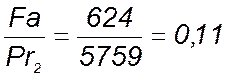
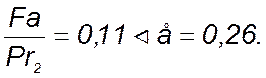
Следовательно выбираем коэффициенты x и у по [1, табл. 9.18]: х = 1; у = 0.

4.  Определяем долговечность подшипников в 1000000 оборотов.

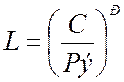                                            (152)

где: С=16800 Н [1, приложение 3].

 Р=3 – показатель степени для шариков подшипников.

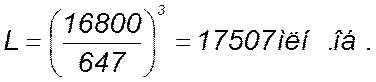
Определяем долговечность подшипника в часах:

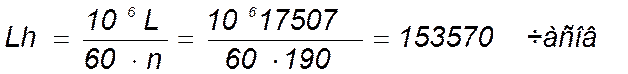    (153)

где n – частота вращения вала.

.

Долговечность и работоспособность подшипников обеспечена.

Вал № 4:

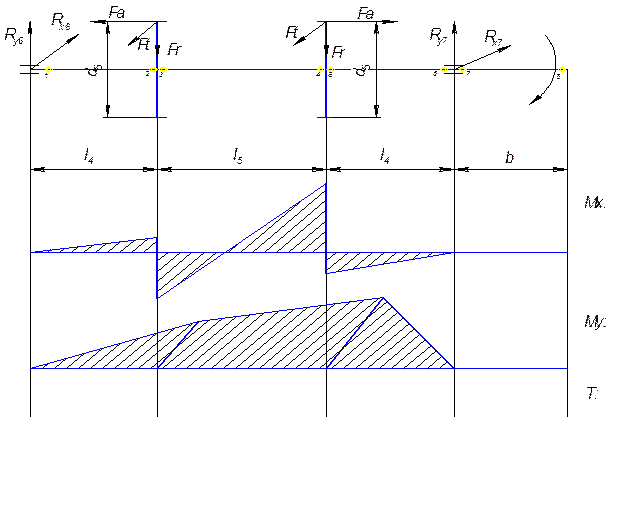
Рисунок 2: Схема нагружения ведомого вала и эпюры изгибающих и крутящего момента

Где:  Ft= 5781Н; Fa= 2375Н; Fr= 1513Н; l₄ = 55мм; l₅ = 150 мм;d₅=256мм.

Определяем силы реакции в подшипниках из условия равновесия:

;

;

;

;

Для подшипника 1 сумма моментов всех сил относительно оси х:

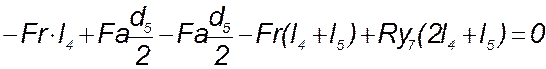    (154)

Из уравнения (154) следует:

 

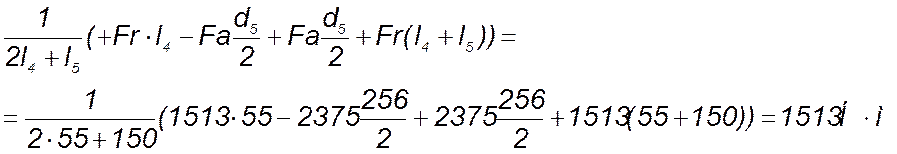
Для подшипника 2 сумма моментов всех сил относительно оси х: .

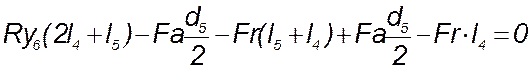                (155)

Из уравнения (155) следует:

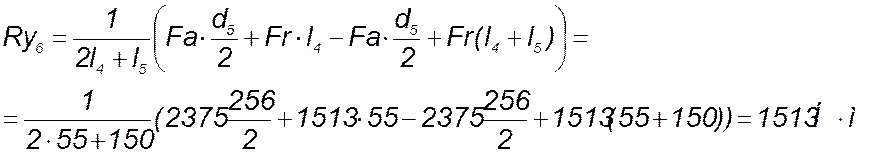(156)

Проверяем условие равновесия:

                            (157)

Условие выполняется.

Для подшипника 6 сумма всех моментов относительно оси у:

        (158)

Из уравнения (158) следует:

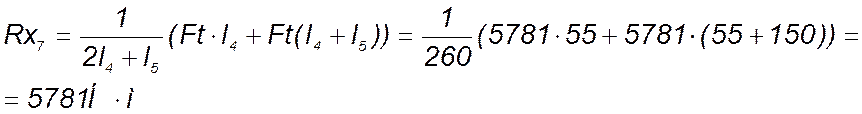          (159)

Для подшипника 7 сумма всех моментов относительно оси у:

        (160)

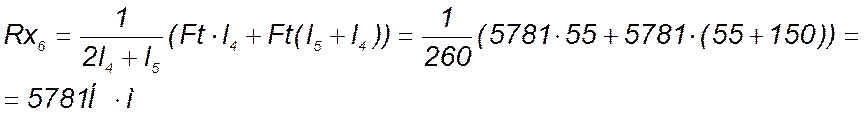         (161)

Проверяем условие равновесия:

                               (162)

Условие равновесия выполняется.

5.  Построение эпюр изгибающих и крутящего момента.

Эпюры моментов строим на сжатых волокнах.

Строим эпюру изгибающих моментов относительно оси х (методом контурных точек).

Мх:

Мх₁=0;

Мх₂=

Мх₃=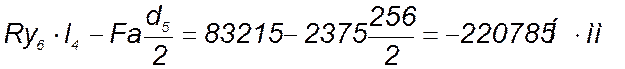

Мх₄=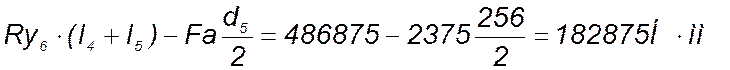

Мх₅=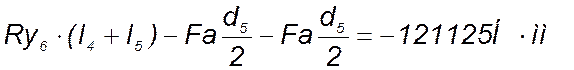

Мх₆=Мх₅

Мх₇=Мх₈

Строим эпюру изгибающих моментов относительно оси у (методом контурных точек).

Му:

Му₁=0.

Му₂=Му₃=

Му₄=Му₅=

Му₆=Му₇=Му₈=0.

6.  Определяем суммарные реакции в подшипниках.

                    (163)

                    (164)

7.  Выбираем подшипники радиальные шариковые однорядные

[1,с. 392]: 113.

Проверяем грузоподъемность и долговечность подшипника по наиболее нагруженной опоре №1.

Определяем эквивалентную нагрузку действующую на подшипники.

где: Кσ =1, - коэффициент, условий работы подшипников;

        Кτ =1, - коэффициент, учитывающий температуру;

V = 1, - Коэффициент, связанный с вращением внутреннего кольца подшипника.

Fa = Fa =2375H.

Определяем отношения:

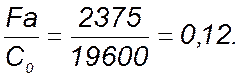
где: С₀ = 19600 Н – статическая грузоподъемность подшипника 113 [1, приложение3].

Тогда по [1, табл. 9.18] определяем е=0,3 – коэффициент осевого нагружения.

Определяем отношение Fa к Pr (на наиболее нагруженный подшипник):

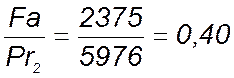
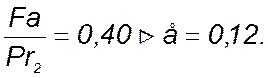
Следовательно выбираем коэффициенты x и у по [1, табл. 9.18]: х = 0,56; у =1,45.

8.  Определяем долговечность подшипников в 1000000 оборотов.

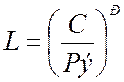                                            (165)

где: С=30700 Н [1, приложение 3].

 Р=3 – показатель степени для шариков подшипников.

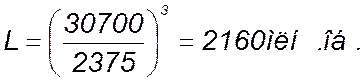
Определяем долговечность подшипника в часах:

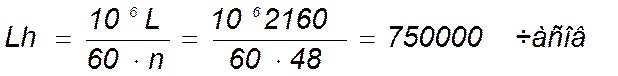    (166)

где n – частота вращения вала.

.

Долговечность и работоспособность подшипников обеспечена.