Теорема штурма. Применение метода Штурма к многочлену. Теоремы о числе действительных корней. Метод Ньютона

является наименьшей степенью неизвестного х, входящей в многочлен л (х) с отличным от нуля коэффициентом. Скобка

(аоХП + +

случайно может состоять при этом лишь из одного слагаемого, а именно тогда, когда КВ-                Аналогичное замечание приме-

нимо и к другим скобкам формулы (5).

Запишем теперь многочлен, равный произведению (х— с) Г (х), причем будем выделять лишь члены, содержащие х в степенях

(X—c)f(X) (аохП+1+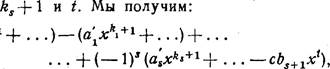

где  д— s, и поэтому, так как с>О, все а „ строго положительны.. Таким образом, в системе коэффициентов многочлена f(x) между членами аох^п и — 01 x^hl (а также между членами'—a1X^k1 и 02x^k2 и т. д.) была одна перемена знаков, а у многочлена (х— с) f(x) между соответствующими членами аох^П + ¹ и  (соответственно между членами —а'х 1

будет или одна перемена знаков, или больше, но тогда непременно на чет ное число. Точные места этих перемен знаков нас не будут при этом интересовать; может случиться, например, что коэффициент при ХА +2 в (В) отрицателен, как и коэффициент -— щ, а поэтому между этими двумя соседними коэффициентами нет перемены знаков, т. е. в первой скобке перемены знаков расположены где-то раньше. Заметим теперь, что последняя скобка в (5) не содержала никаких перемен знаков, в то время как последняя скобка в (6) их содержит, притом н ечетн ое число: достаточно учесть, что последние отличные от нуля коэффициенты многочленов f(x) и (х— с) Г т, е. s +1 c , имеют разные знаки. Таким образом, при переходе от / (х) к (X—c)f(x) общее число перемен знаков в системе коэффициентов непременно увеличивается, притом на нечетное число (сумма нескольких слагаемых, одно из которых нечетно, а остальные четны, будет, ПОНЯТНО, нечетной!). Лемма доказана,

Для доказательства теоремы Декарта обозначим через Ч, . . . , ак все положительные корни многочлена Г Таким образом,

                     Г (х) = (х—ал) (х—ая)         (х—ак) ф (х),

где ф (х)—многочлен с действительными коэффициентами, уже не имеющий положительных действительных корней. Отсюда следует, что первый и последний отличный от нуля коэффициенты многочлена (Р (х) одного знака, т. е. система коэффициентов этого многочлена содержит четное число перемен знаков. Применяя теперь доказанную выше лемму последовательно к многочленам

 (Х), (х—а1) ф (Х), (х—ч) (х—а2) (Х),

мы получим, что число перемен знаков в системе коэффициентов каждый раз увеличивается на нечетное число, т. е. на единицу плюс четное число, а поэтому число перемен знаков в системе коэффициентов многочлена Г (х) больше числа К на четное число.

Применим теоремы Декарта й Бюдана — Фурье к рассматривавшемуся выше многочлену

                                     (Х)           +2Х⁴ —5Х³ + — 7Х — З.

Число перемен знаков в системе коэффициентов равно трем, и поэтому, по теореме Декарта, h (х) может иметь три или один положительный корень. С другой стороны, h (х) не имеет равных нулю коэффициентов, а так как в системе коэффициентов два сохранения знаков, то h (х) либо имеет два отрицательных корня, либо не имеет ни одного. Сравнивая с результатами, полученными ранее бри помощи графика, мы получаем, что два есть точное число отрицательных корней нашего многочлена.

Для точного определения числа положительных корней воспользуемся теоремой Бюдана—Фурье, причем применим ее к отрезку (1, х), так как в S 39 уже было показано, что 1 служит нижней границей положительных корней многочлена .h (х). Последовательные производные [г (х) также уже были выписаны в S 39. Найдем их знаки при х— 1 и х— Ф :

	(х)	h' (х)	(х)	h”' (х)	h IV (х)	hV (х)	Число перемен знаков
			-6-

Отсюда следует, что система производных теряет при переходе х от 1 до оо одну перемену знаков, а поэтому 11 (х) имеет ровно один положительный корень.

В связи с этим примером заметим, что вообще при разыскани и числа дейс т в ительных ко ру ей многочлена следует начинать с построения гр афика и при м ен ения тео ре м Декарта и Бюдана—Фу рье, лишь в к р айних сл уч аях переходя к по строению системы Штурма.

Теорема Декарта допускает некоторое уточнение в том частном случае, когда заранее известно, что все корни многочлена действительные, как это имеет место, например, для характеристического многочлена симметрической матрицы. Именно:

Если все корни ЛНOГOЧЛеНа f(x) Действительные, а свободный член отличен от нуля, то число К! положительных корней этого многочлена ра вно числу s1 перелен знаков в системе его коэффициентов, а число К2 отрицательных корней равно числу пережен знаков в системе коэффициентов многочлена

Действительно, при наших предположениях

                                                                                                          (7)

где п— степень многочлена Г (х), и, по теореме Декарта,

(8)

Докажем, что

                                                                                                           (9)

Доказательство будем вести индукцией по п, так как при п = 1 ввиду ао+О, Ч +0 перемена знаков имеется лишь у одного из многочленов

Г (х) = аох -1- Ч,  —аох4-

т. е. для этого случая -FS2 1. Пусть формула (9) уже доказана для многочленов, степень которых меньше п. Если

(х) = аох^п + ав_

42]

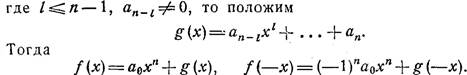
Если s 1 и s2 будут соответственно числа перемен знаков в системах коэффициентов многочленов g (х) и g(—x), то, по индуктивному предположению (ясно, что 1),

Если то перемена знаков на первом месте, т. е., дЛЯј^С (Х), между ао и будет лишь у одного из многочленов