Характеристические корни и собственные значения. Линейные подпространства. Определение евклидова пространства. Ортонормированные базы

полученных результатов и доказанной выше формулы (2) вытекает утверждение теоремы.

Невырожденные линейные преобразования. Линейное преобразование линейного пространства Vn называется невырожДенныл, если оно удовлетворяет любому из следующих условий, равносильность которых немедленно вытекает из доказанных выше теорем: 1.. Ранг пре образ ован ия равен п.

2. Областью з н а чений преобразования ф служит в с е п р ост р ан ст в о

З. Дефект преобр азования (Р равен нулю.

Для невырожденных линейных преобразований можно указать также много других определений, равносильных указанным выше, в частности определения 4—6.

4.  Р а зличные. векторы п р о ст ранств а Vn имеют пр и п р еобразов а н и и различные образы.

Действительно, если преобразование ф обладает свойством 4, то ядро этого преобразования состоит лишь из нулевого вектора, т. е. выполняется и свойство З. Если же векторы а и Ь таковы, что а + Ь, но аф=Ьф, то  но  т. е. свойство З не выполняется.

Из 2 и 4 вытекает

5.  Преобразова н ие явля ет с я взаимно одноз на ч ны м отображением п рост ра нства Уп н а все это пр о с т р а н ств о.

Из 5 следует, что для невырожденного линейного преобразования существует обратное преобразование (р- ¹ , переводящее всякий вектор ар в вектор а,

Преобразование ф -1 будет линейным, так как (ар + Ьф) —1 _ + Ь) ср

[а (ap.)lrp -1 — [(aa)wl ф -1 = ша.

Из определения преобразования ф -1 вытекает, что

                                                                           (11)

равенства (11) могут сами рассматриваться как определение обратного преобразования. Отсюда и из последних результатов предшествующего параграфа следует, что если невырожденное линейное преобразование задается в некоторой базе латрицей А, невырожденной ввиду свойства 1, то преобразование (Р -1' заДаелся в этой базе матрицей

Мы приходим, таким образом, к следующему определению невырожденного линейного преобразования:

 6. Для прео бразования (Р существует обратное линейное преобразование ф—1

S 33. Характеристические корни и собственные значен'ия

Пусть квадратная матрица порядка п с действительными элементами. Пусть, с другой стороны, Х— некоторое неизвестное. Тогда матрица А—ЛЕ, где Е— единичная матрица порядка п, называется характеристической жатрицей матрицы А, Так как в матрице ЯЕ по главной диагонали стоит Л, все же остальные элементы равны нулю, то

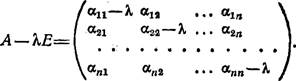
Определитель матрицы будет многочленом от Я, притом степени п. В самом деле, произведение элементов, стоящих на главной диагонали, будет многочленом от Л со старшим членом 1 УР, все же остальные члены определителя не содержат по меньшей мере двух из числа элементов, стоящих на главной диагонали, и поэтому их степень относительно Х не превосходит п—2. Коэффициенты этого многочлена можно было бы легко найти. Так, коэффициент при равен ( — а свободный член совпадает с определителем матрицы А.

Многочлен п-й степени 1 А ЛЕ! называется характеристически.н многочленом матрицы А, а его корни, которые могут быть как действительными, так и комплексными, называются характеристиескими корнями этой матрицы.

Подобные латрицы обладают оДинаковыми характеристическижи многочленами и, слебовательно, одинаковыми характеристическижи корнями,

831 ХАРАКТЕРИСТИЧЕСКИЕ КОРНИ И СОБСТВЕННЫЕ ЗНАЧЕНИЯ

Пусть, в самом деле,

B=Q-1AQ.

Тогда, учитывая, что матрица ЖЕ перестановочна с матрицей Q,

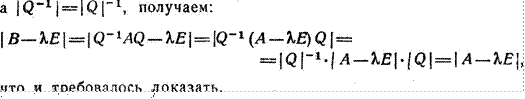
Из этого результата вытекает, ввиду доказанной в S 31 теоремы о связи между матрицами, задающими линейное преобразование в разных базах, что хотя линейное преобразование ложет заДаваться в разных базах различными латрицали, оДнако все эти матрицы имеют один и тот же набор характеристическИХ корней. Эти корни можно называть поэтому характеристическИ.ИИ корнями самого преобразования Ч). Весь набор этих характеристических корней, причем каждый корень берется с той кратностью, какую он имеет в характеристическом многочлене, называется спектрол линейного преобразования ф.

Характеристические корни играют при изучении линейных преобразований очень большую роль. Читатель много раз будет иметь возможность в этом убедиться. Одно из применений характеристических корней мы сейчас укажем.

Пусть в действительном линейном пространстве           задано линейное преобразование ф. Если вектор Ь, отличный от нуля, переводится преобразованием в вектор, пропорциональный самому Ь, bw=iob,           (1)

где Хо— некоторое действительное число, то вектор Ь называется