Конструирование привода рабочего органа. Сборочный чертёж. Чертёж выходного вала редуктора. Чертёж зубчатого колеса

Определение коэффициента, учитывающего суммарную длину      контактной линии

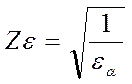                                                         ,                                             [3]

где  e_a - коэффициент торцевого перекрытия зубьев

                                e_a = [1,88-3,2 × (1/z₁+1/z₂)],                                 [3]

e_a = [1,88-3,2 × (1/35+1/98)] = [1,88-3,2 × (0,02+0,01)] = 1,76

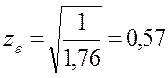
Полученные значения подставляем в формулу

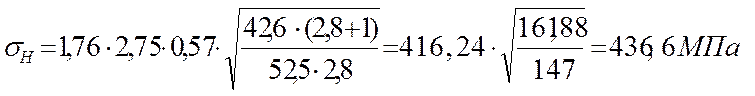
3.11  Определение перегрузки передачи

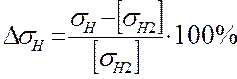                                      ,                                               [3]

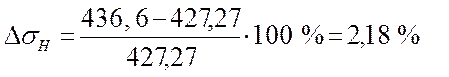
Что не превышает 5%.

3.12  Определение изгиба для наиболее слабого звена

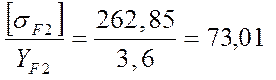
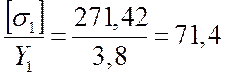
Наиболее слабое звено – колесо, так как у него отношение [s_F] /Y_F меньше чем у шестерни.

3.13  Определение напряжения изгиба у ножки зуба

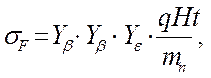
где Y_F - коэффициент формы зуба, Y_F=0,98;

Y_b - коэффициент, учитывающий перекрытие зубьев, Y_b = 0,98;

Y_e - коэффициент, учитывающий перекрытие зубьев, Y_e = 1;

qFt – удельная расчетная окружная сила изгиба.

	21

 

3.13.1  Определение удельной расчетной окружной силы изгиба

                                       qFt = F_t × К_Fa × К_Fb × КFv/b₂  ,                                    [3]

Принимаем К_Fa=1,07; КFv = 1,13; К_Fb = 1,26

qFt = 1695 × 1,07 × 1,26 × 1,13/49 = 51,78 н/ мм

Полученные значения подставляем в формулу

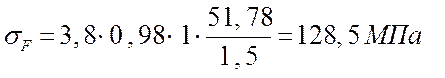
Таким образом, полученное в результате расчета напряжение значительно меньше допустимого.

s_F=128,5 МПа < [s_F] = 262,85 МПа

	22

 

4 Расчет валов редуктора

4.1 Выбор материала валов

Для всех валов принимаем  материал - сталь 45, размер заготовки любой, с механическими характеристиками: твердость – 200 НВ, s_В = 560МПа,  s_Т = 280 МПа, s_-1 = 250 МПа, t_-1 = 150 МПа, Y_s = 0.

4.2 Ориентировочный расчет валов

4.2.1 Определение диаметра входного вала

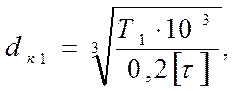                                                                                        [4]

где Т₁ – крутящий момент на валу, Н×м;

[t] - допускаемое касательное напряжение, принимаем [t]=25 Мпа;

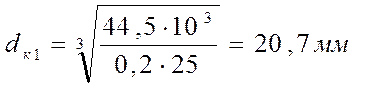
По ГОСТу принимаем d_к1 = 21 мм. Далее определяем диаметры на остальных участка вала.

                                                       d_y1 = d_k1+2,                                               [4]

d_y1 = 21+2 = 23 мм

                                                       d_п1 = d_y1+5,                                               [4]

d_п1  = 23+5 = 28 мм

                                                      d_з.к1.= d_п1+3,                                               [4]

d_з.к1 = 28+3 = 31мм

                                                      d_б1 = d_з.к1+2,                                               [4]

d_б1 = 31+2 = 33 мм

4.2.2 Определение диаметра выходного вала

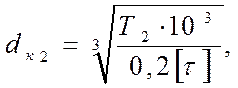                                                                                 [4]

где Т₂ – крутящий момент на валу, Н×м

	23

 

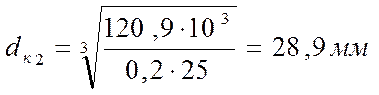
По ГОСТу принимаем d_к2 = 30 мм, и определяем диаметры на остальных участка вала.

                                                      d_y2 = d_k+2,                                               [4]

d_y1 = 30+2 = 32 мм

                                                     d_п2 = d_y2+5,                                              [4]

d_п1  = 32+5 = 37 мм

                                                     d_з.к2.= d_п2+3,                                             [4]

d_з.к1 = 37+3 = 40 мм

                                                     d_б2 = d_з.к2+2,                                             [4]

d_б2 = 40+2 = 42 мм

Далее выполняем эскизную компоновку редуктора, по окончании которой определяем расстояние между силами, приложенными к валу и реакции опор, l₁=0,043 м; l₂=0,043 м; l₃=0,035 м.

4.3 Проверочный расчет входного вала на статическую прочность

4.3.1 Определение реакций опор в точках А и В

SМ_В=0,

-  R_AX(l₁+l₂) – F_r × l₂ = 0,

Отсюда

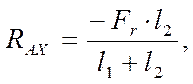                                                                                       [4]

где F_r – радиальное усилие, Н;

l₁, l₂ – расстояние между силами, м.

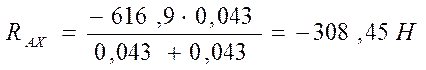
R_BX(l₁+l₂) – F_r × l₁ = 0

Отсюда

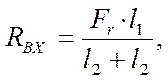                                                                                      [4]

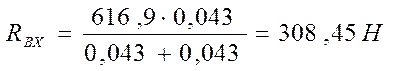
Проверка

                                                  R_AX +F_r-R_BX=0,                                          [4]

-308,45+616,9-308,45 = 0

 

4.3.2  Определение изгибающих моментов по нагруженным участкам в вертикальной плоскости XAZ

0£ Z₁£l₁,

                                                   M_y1 = R_AX × Z₁,                                          [4]

Z₁ = 0,   M_Y1 = 0,

Z₁ = l₁,   M_y1 = R_AX × l₁=- 308,45 × 0,043 = -13,26 H×м

0£ Z₂£l₂,

                                         M_y2 = R_AX (l₁+Z₂) + F_r  ×l₂,                                   [4]

Z₂ = 0,   M_y2 = -308,45 × 0,043 = 13,26 Н×м

Z₂ = l₂,   M_y2 = -308,45×(0,043+0,043)+616,9×0,043=-26,52+26,52 = 0

По полученным данным строим эпюру изгибающих моментов.

4.3.3  Определение реакций опор в плоскости YAZ

SМ_В=0,

-R_AY(l₁+l₂) + F_t × l₂ = 0,

   Отсюда

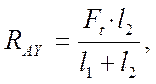                                                                                [4]

   где F_t – окружное усилие на первом валу, Н;

  

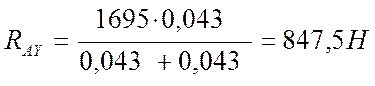
   SМ_А = 0,

   R_ВY(l₁+l₂) – F_t × l₁ = 0

   Отсюда

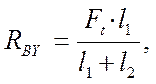                                                                                         [4]                                                                                                                                                                                

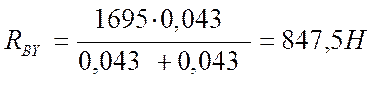
Проверка

-R_AY+F_t-R_BY = 0,

-847,5+1695-847,5 = 0

	25

 

4.3.4 Определение изгибающих моментов по нагруженным участкам вала в горизонтальной плоскости YAZ

0£ Z₁£l₁,

                                                    M_X1=R_AY × Z₁,                                          [4]

Z₁ = 0,   M_X1  = 0,

Z₁  = l₁,   M_X1 = 847,5 × 0,043 = 36,44 Н×м

0£ Z₂£l₂,

                                           M_X2=R_AY(l₁+Z₂)-F_t×Z₂,                                      [4]

Z₂ = 0,   M_X2  = 847,5 × 0,043 = 36,44 H×м

Z₂=l₂,   M_X2= -847,5 × 0,086+1695 × 0,043=0

По полученным значениям строим эпюру изгибающих моментов.

4.3.4  Определение величин суммарных изгибающих моментов в сечениях вала

                                                                                [4]

М_и1 = 0

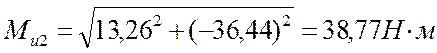
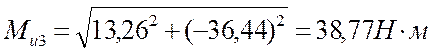
М_и4 = 0,

По полученным данным строим эпюру изгибающих моментов

4.3.5  Определение момента в опасном сечении

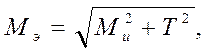                                                                                  [4]

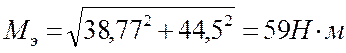
Уточняем диаметр вала в опасном сечении под колесом 

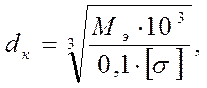                                                                             [4]

где М_э – эквивалентный момент в опасном сечении, Н × м;

[s] - допускаемое напряжение при изгибе, [s] = 50 МПа.

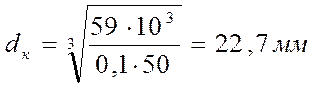
Расчет показал, что диаметр вала необходимо уменьшить d_п=25 мм, d_з.к.=30 мм, d_б=35 мм, d_к=20 мм.   

	26

 

RAX

X

RBX

 

 

                                                                  

Рисунок 4.1 – Схема к расчету

	27

 

4.4  Проверочный расчет  выходного вала на статическую прочность

4.4.1   Рассчитываем реакции опор в точках А и В из условий равновесия

SМ_В=0,

-  R_AX(l₁+l₂) + F_r × l₂+R × l₃ = 0,

Отсюда

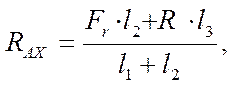                                                                                     [4]

где F_r – радиальное усилие, Н;

l₁, l₂, l₃ – расстояние между силами, м;

R –  сила давления на вал в цепной передаче, Н.

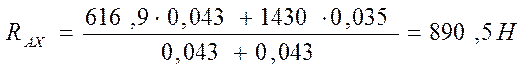
SМ_А = 0,

R(l₁+l₂+l₃) - R_BX(l₁+l₂) – F_r × l₁ = 0

Отсюда

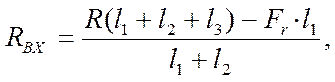                                                             [4]

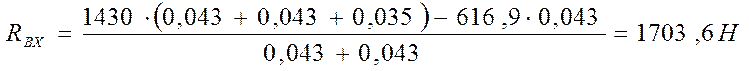
Проверка

R_AX -F_r-R_BX+R=0,

890,5-616,9-1703,6+1430=0

4.4.2  Определение изгибающих моментов по нагруженным участкам в вертикальной плоскости XAZ

0£ Z₁£l₁,

                                                     M_y1 = R_AX × Z₁,                                        [4]

Z₁ = 0,   M_Y1 = 0,

Z₁ = l₁,   M_y1 = R_AX × l₁= 890,5 × 0,043 = 38,29 H×м

0£ Z₂£l₂,

                                          M_y2 = R_AX (l₁+Z₂) – F_t×Z₂,                                      [4]

Z₂ = 0,   M_y2 = 890,5 × 0,043 = 38,29 Н×м

Z₂ = l₂,   M_y2 = 890,5×(0,043+0,043)-616,9×0,043=76,58-26,52 = 50,06 Н×м

	28

 

0£ Z₃£l₃,

                                            М_y3=R×Z₃,                                                  [4]

Z₃=0,    M_y3=0,

Z₃=l₃     M_y3=1430 × 0,035=50,06 Н × м

По полученным данным строим эпюру изгибающих моментов.

4.4.3  Определение реакций опор в плоскости YAZ

SМ_В=0,

-R_AY(l₁+l₂) + F_t × l₂ = 0,

   Отсюда

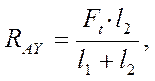                                                                                    [4]

   где F_t – окружное усилие на втором валу, Н;

  

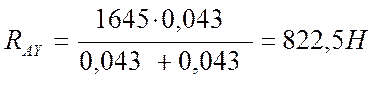
   SМ_А = 0,

   R_ВY(l₁+l₂) – F_t × l₁ = 0

   Отсюда

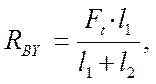                                                                                       [4]

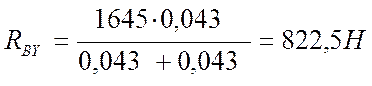
Проверка

-R_AY+F_t-R_BY = 0,

-822,5+1645-822,5 = 0

 

4.4.4  Определение изгибающих моментов по нагруженным участкам вала в горизонтальной плоскости YAZ

0£ Z₁£l₁,

                                           M_X1=R_AY × Z₁,                                          [4]

Z₁ = 0,   M_X1  = 0,

Z₁  = l₁,   M_X1 = 822,5 × 0,043 = 35,36 Н×м

0£ Z₂£l₂,

                                  M_X2=R_AY(l₁+Z₂)-F_t×Z₂,                                         [4]

	29

 

Z₂ = 0,   M_X2  = 822,5 × 0,043 = 35,36 H×м

Z₂=l₂,   M_X2= -822,5 × 0,086+1645 × 0,043=0

По полученным значениям строим эпюру изгибающих моментов.

4.4.5  Определение величин суммарных изгибающих моментов в сечениях вала

                                                                              [4]

М_и1 = 0

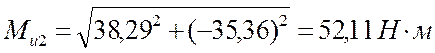
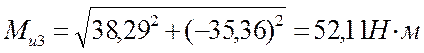
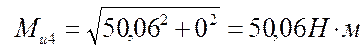
М_и5 = 0,

По полученным данным строим эпюру изгибающих моментов

4.4.6  Определение момента в опасном сечении

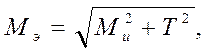                                                                                [4]

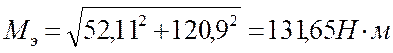
Уточняем диаметр вала в опасном сечении под колесом 

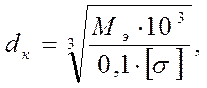                                                                                [4]

где М_э – эквивалентный момент в опасном сечении, Н × ;

[s] - допускаемое напряжение при изгибе, [s] = 50 МПа.

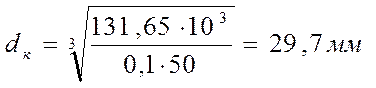
Принимаем d_п=25 мм и корректируем значения d_з.к.=30 мм, d_б=35 мм, d_к=20 мм.   

 

 

35,36

                                                                                                    

 

Рисунок 4.2 – Схема к расчету

31

 

4.5  Уточненный расчет выходного вала на усталостную прочность

Опасное сечение вала располагается под колесом. На этом этапе необходимо  оценить усталостную прочность.

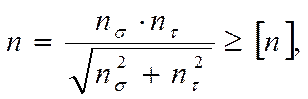                                                             [4]

где n_s - коэффициент усталостной прочности при изгибе;

n_t - коэффициент усталостной прочности при кручении.

[n] - допускаемый коэффициент запаса прочности.

Коэффициент усталостной прочности при изгибе и при кручении:

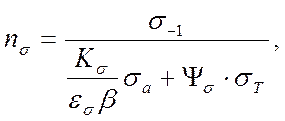                                                                [4]

где s_-1 - предел выносливости стали при симметричном цикле изгиба;

К_s - эффективный коэффициент концентрации нормальных                      напряжений при изгибе;

e_s - масштабный фактор для нормальных напряжений при изгибе;

b - коэффициент учитывающий влияние шероховатости поверхности при изгибе;

s_а - амплитуда цикла нормальных напряжений при изгибе, МПа;

s_Т  - среднее напряжение цикла нормальных напряжений при изгибе;

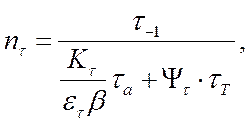                                                                     [4]

где где t_-1 - предел выносливости стали при симметричном цикле кручения;

К_t - эффективный коэффициент концентрации нормальных                      напряжений при кручении;

e_t - масштабный фактор для нормальных напряжений при кручении