





Министерство Образования Российской Федерации
Сибирский Государственный Технологический Университет
Факультет: Механический
Кафедра математики и информатики
ПРАКТИЧЕСКИЕ РАБОТЫ
По дисциплине: Математические методы в инженерии
Вариант 4
|
Руководитель: _______________ (подпись) _________________________________ (оценка) (дата) |
|
|
Выполнил: студент гр. 92-01 _______________ (подпись) _______________ (дата) |
КРАСНОЯРСК, 2012
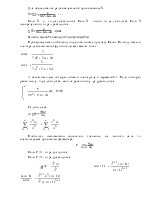
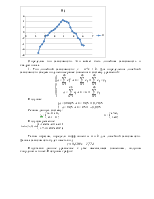
1. Построить график функции:
а) ![]()
Присваиваем функции у(х) значение:
![]()
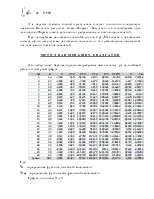
На панели инструментов «График» выбираем график в декартовой системе координат. В маркер горизонтальной оси задаем значение переменной х, а вертикальной оси, имя функции у(х), а также диапазон значений по осям:
|
|
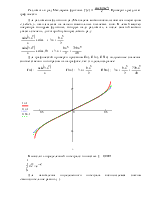
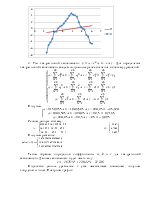
б) 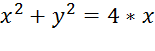
При помощи команды «Символика → Переменная → Решить»
находим значения у в точках ![]() и
и ![]() :
:
|
|
Присваиваем функции значение в каждой точке:
|
|
|
|
На панели инструментов «График» выбираем график в декартовой системе координат. В маркер горизонтальной оси задаем значение переменной х, а вертикальной оси, имена функций у1(х) и y2(x) через запятую, а также диапазон значений по осям:
|
|
2. Решить уравнение:
а) 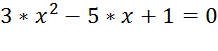 ;
;
Выделяем переменную х, выполняем команду «Символика → Переменная → Решить».
|
|
б)
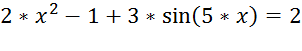 ;
;
Выполним операцию, аналогичную предыдущей. Получим решение уравнения:
|
|
в)
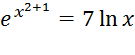
Присваиваем некоторой переменной а данное уравнение через оператор «root», перенеся все значения в одну сторону. Указываем после запятой, что решение будем производить по переменной х:
|
|
Находим значение переменной а через вычислительное равно. Полученное значение и будет являться решением данного уравнения:
|
|
3. Решить систему уравнений:
а)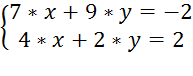
Данную систему линейных уравнений можно решить с помощью блока Given - Find (Дано - Найти). Для этого в первую очередь под оператор Given (Дано) задаем два уравнения, прописывая их через знак «жирное равно»:
|
|
|
|
|
|
Затем в столбец сводим искомые величины и присваиваем их оператору Find (Найти) с заданием названия переменной:
|
|
После чего через «вычислительное равно» находим значения a и b, соответствующих x и y.
|
|
|
|
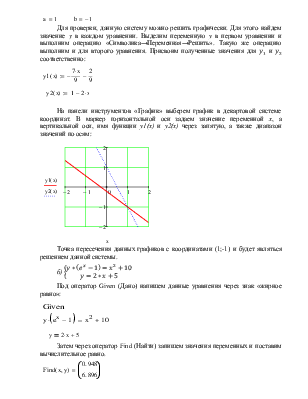
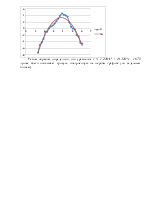
Для проверки, данную систему можно решить графически.
Для этого найдем значение y в каждом уравнении. Выделим переменную у
в первом уравнении и выполним операцию «Символика→Переменная→Решить». Такую же
операцию выполним и для второго уравнения. Присвоим полученные значения для ![]() и
и ![]() соответственно:
соответственно:
|
|
|
|
На панели инструментов «График» выберем график в декартовой системе координат. В маркер горизонтальной оси задаем значение переменной х, а вертикальной оси, имя функции у1(х) и у2(х) через запятую, а также диапазон значений по осям:
|
|
Точка пересечения данных графиков с координатами (1;-1) и будет являться решением данной системы.
б) 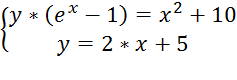
Под оператор Given (Дано) напишем данные уравнения через знак «жирное равно»:
|
|
|
|
|
|
Затем через оператор Find (Найти) запишем значения переменных и поставим вычислительное равно.
|
|
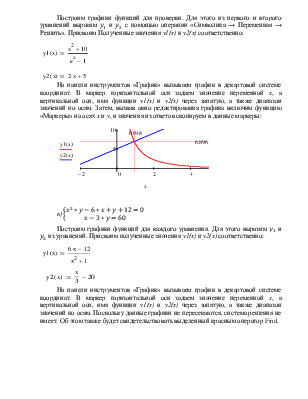
Построим графики функций для проверки. Для этого из
первого и второго уравнений выразим ![]() и
и ![]() с помощью операции «Символика → Переменная → Решить».
Присвоим Полученные значения у1(х) и у2(х) соответственно:
с помощью операции «Символика → Переменная → Решить».
Присвоим Полученные значения у1(х) и у2(х) соответственно:
|
|
|
|
На панели инструментов «График» вызываем график в декартовой системе координат. В маркер горизонтальной оси задаем значение переменной х, а вертикальной оси, имя функции у1(х) и у2(х) через запятую, а также диапазон значений по осям. Затем, вызвав окно редактирования графика включим функцию «Маркеры» на осях х и у, и значения из ответов скопируем в данные маркеры:
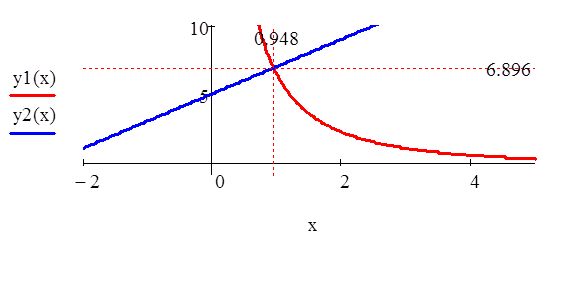
в) 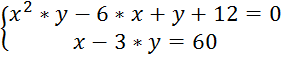
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.